Decision Theory and Motion Planning
Motion planning and decision making are at the core of Robotics and A.I. In theory, these problems can be solved using optimal control or dynamic programming. However, computational cost for solving many real world problems is prohibitively high and is exacerbated by the “curse of dimensionality”. Randomized sampling-based methods (like RRT*) ameliorate this problem by avoiding apriori griding of the environment and incrementally building a graph online. On the other hand, deterministic search algorithms (such as A*) can be augmented with intelligent abstractions to speed up their performance, and decision theory can borrow ideas from information theory to model agents that are resource-aware. Current research in this area lies at the intersection of A.I, machine learning, optimal control and information theory.
Sampling-based Algorithms for Optimal Motion Planning
Motion planning and trajectory generation problems are at the at the core of all autonomous and robotic systems. Although – at least in theory – such problems can be solved using optimal control or dynamic programming, the computational complexity for realizing these solutions is still prohibitive for many real-life problems, especially for high-dimensional systems. Recently, randomized algorithms have been proposed, which promise to remedy the “curse of dimensionality” associated with more traditional, deterministic methods.
Information Theoretic Abstractions and Decision Making

Multi-Agent Multi-Scale Path Planning
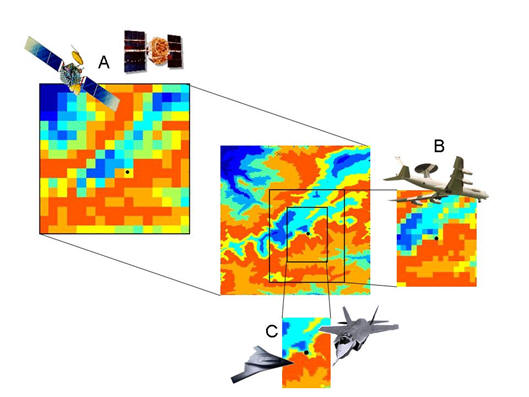 Although complete knowledge of the environment is necessary to plan an optimal solution for given task, the information about the world in which a planning agent is to plan is rarely entirely known. More likely, the agent has only a glimpse of the world abstracted away from the current state and time. This idea has led many researchers to wonder how to abstract the search space in an efficient and meaningful way. Since the early days of AI, a hierarchical abstraction of a transition system has been recognized as a crucial tool for planning in complex environments and long decision horizons.
Although complete knowledge of the environment is necessary to plan an optimal solution for given task, the information about the world in which a planning agent is to plan is rarely entirely known. More likely, the agent has only a glimpse of the world abstracted away from the current state and time. This idea has led many researchers to wonder how to abstract the search space in an efficient and meaningful way. Since the early days of AI, a hierarchical abstraction of a transition system has been recognized as a crucial tool for planning in complex environments and long decision horizons.
Game Theory
Game theory provides for a mathematical framework to study optimal decision making in multi-agent decision making problems. It provides a rich framework to study situations ranging from competitive and strategic encounters between agents to cooperative, team-game, scenarios. However, research within this field has been mainly concerned with cases where each player/agent has perfect and symmetric knowledge of the environment or understanding of the game at hand. In our research, we seek to progressively relax these assumptions, and to model real-world scenarios where agents may not all be created equal - that is, not all have the same ability or understanding of the evolution of the system dynamics, etc. We employ results from machine learning, theoretical game theory and optimization theory to model, solve and establish theoretical results from this new field of research.
Level-K Thinking for Pursuit-Evasion Games
Pursuit-Evasion Game (PEG) models a family of problems in which one group of agents attempt to track down members of another group in an environment. This type of problem has a variety of applications in military and civil fields, for example, an adversary aerial combat or a surveillance/tracking mission. Over the past decades, people strive to solve for the equilibrium of such games, either Nash equilibrium or the correlated equilibrium, where all the agents are assumed to be totally rational. However, the equilibrium is generally hard to solve and may require a significant amount of computational time. In reality, agents (both autonomous agents and humans) only have limited computational capacity, limited information and limited time. As a result, critiques of the perfect rationality assumption in the notion of equilibrium arose, and people want to introduce the idea of bounded rationality.
Pursuit-Evasion Games under Lack of Common Knowledge
Pursuit-evasion games have traditionally been studied under the assumption that both player have an identical understanding of the environment in which they operate. However this is rarely true in practice. Instead, players form their own understanding of the dynamics of the world. This discrepancy in the understanding of the evolution of the system may arise due to sensing limitations or because of the agent's prior experience or may also be due to deception, measurement capability of the agent or erroneous modeling assumptions of the environment.
Min-Max Differential Dynamic Programming
Design of a robust controller formalized as a $\mathcal{H}_\infty$ control problem has been successfully extended with min-max game theoretic formulation to cope with model uncertainty and external disturbances. Such attempts were derived in the context of the small gain theorem to ensure the system stability under unstructured perturbations, and recently applied to dynamic programming algorithms to solve for the locally optimal trajectory with robustness guaranteed.
Selected Publications
- Tsiotras, P., and Bakolas, E.,"A Hierarchical On-Line Path-Planning Scheme Using Wavelets,'' European Control Conference, Kos, Greece, July 2-5, 2007.
- Tsiotras, P., "Multiresolution Hierarchical Path-Planning for Small UAVs,'' European Control Conference, Kos, Greece, July~2-5, 2007 (invited)
- Cowlagi, R. and Tsiotras, P., "Shortest Distance Problems in Graphs Using History-Dependent Transition Costs with Application to Kinodynamic Path Planning,'' American Control Conference, St. Louis, MO, June 10-12, 2009, (best student paper award), pp. 414-419.
- Cowlagi, R. and Tsiotras, P. "Beyond Quadtrees: Cell Decomposition for Path Planning using the Wavelet Transform," 46th IEEE Conference on Decision and Control, New Orleans, LA, Dec. 12-14, 2007, pp. 1392-1397.
- Cowlagi, R., and Tsiotras, P., "Multiresolution Path Planning with Wavelets: A Local Replanning Approach,'' American Control Conference, Seattle, WA, June 1-13, 2008, pp. 1220-1225.
- Bakolas, E., and Tsiotras, P., "Multiresolution Path Planning Via Sector Decompositions Compatible to On-Board Sensor Data,'' AIAA Guidance, Navigation, and Control Conference, Honolulu, HI, Aug. 18-21, 2008, AIAA Paper 2008-7238.
- Cowlagi, R., and Tsiotras, P., "Multi-resolution Path Planning: Theoretical Analysis, Efficient Implementation, and Extensions to Dynamic Environments,'' 49th IEEE Conference on Decision and Control, Atlanta, GA, Dec. 15-17, 2010, pp. 1384-1390.
- Lu, Y., Huo, Y., and Tsiotras, P., "Beamlet-like Data Processing for Accelerated Path-Planning Using Multiscale Information of the Environment,'' 49th IEEE Conference on Decision and Control, Atlanta, GA, Dec. 15-17, 2010, pp. 3808-3813
- Tsiotras, P., Jung, D., and Bakolas, E., "Multiresolution Hierarchical Path-Planning for Small UAVs Using Wavelet Decompositions,'' Journal of Intelligent and Robotic Systems, doi: 10.1007/s10846-011-9631-z
- Lu, Y., Huo, Y., and Tsiotras, P., "An Accelerated Path-Finding Algorithm Using Multiscale Information,'' IEEE Transactions on Automatic Control, 2012
- Lu, Y., Huo, X., Arslan, O., and Tsiotras, P., "An Incremental, Multi-Scale Search Algorithm for Dynamic Path Planning with Low Worst Case Complexity,'' IEEE Transactions on Man, Systems and Cybernetics, Part B: Cybernetics, 2012
- Cowlagi, R. and Tsiotras, P., "Hierarchical Motion Planning with Kinodynamic Feasibility Guarantees,'' IEEE Transactions on Robotics, 2012
- Hauer, F., Kundu, A., Rehg, J., and Tsiotras, P., "Multi-scale Perception and Path Planning on Probabilistic Obstacle Maps,'' IEEE International Conference on Robotics and Automation, Seattle, WA, May 26-30, 2015, pp. 4210--4215, doi:10.1109/ICRA.2015.7139779
- Hauer, F., Tsiotras, P., "Reduced Complexity Multi-Scale Path-Planning on Probabilistic Maps,'' IEEE International Conference on Robotics and Automation, Stockholm, Sweden, May 16-21, 2016, pp. 83-88, doi:10.1109/ICRA.2016.7487119
Contact
For more information contact Daniel Larsson.

