Home | People | Research | Publications | Software | Links | News | Contact   

Multiresolution Path Planning for Autonomous Agents

The current practice in control system design is to develop the control algorithm, without giving any specific thought
to the available hardware required for its implementation. Finding the suitable control hardware to implement the algorithm is an after-the-fact task. For many problems involving embedded control hardware with limited computational resources (both in terms of available CPU and memory) this traditional way of doing things may not be possible. This research aims at reversing this line of thinking and introduce a new paradigm, such that the operational limitations of the hardware become part of the control algorithm design specifications.

As a particular instance of this transformative control design philosophy, the ubiquitous problem of vehicle navigation
in a natural environment full of obstacles will be used. A new multi-resolution algorithm is being proposed to efficiently encode all possible paths inside this environment. The main idea used is the fact that paths have lower dimensionality than the ambient space they lie in, and hence, a more efficient encoding of the problem data than standard 2D and 3D cell decompositions should be possible. As a result, the search space is considerably reduced. The main mathematical tool used is wavelets and beamlets, whose unique properties capture directionality, in addition to scale and locality. The adoption of beamlets enables for numerically more efficient algorithms than previous cell decomposition-only based path planning approaches. As an added benefit of the approach, the typically uncoupled geometric and dynamic planner layers in the motion planning hierarchy can now be naturally coordinated by passing information about the allowable dynamic envelope of the vehicle to the geometric layer. This ensures that the paths computed by the geometric layer will indeed be rendered dynamically feasible.

                      


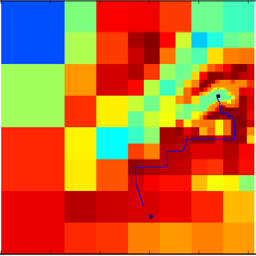
Wavelet Cell Decompositions for Path Planning

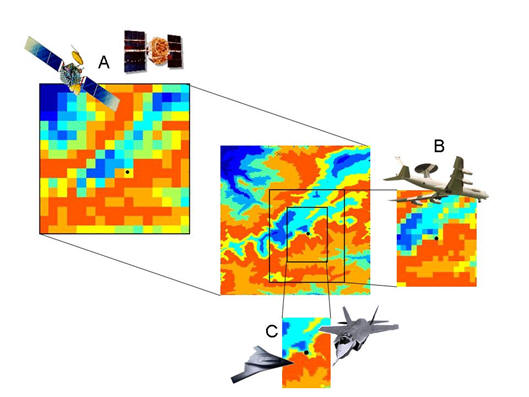
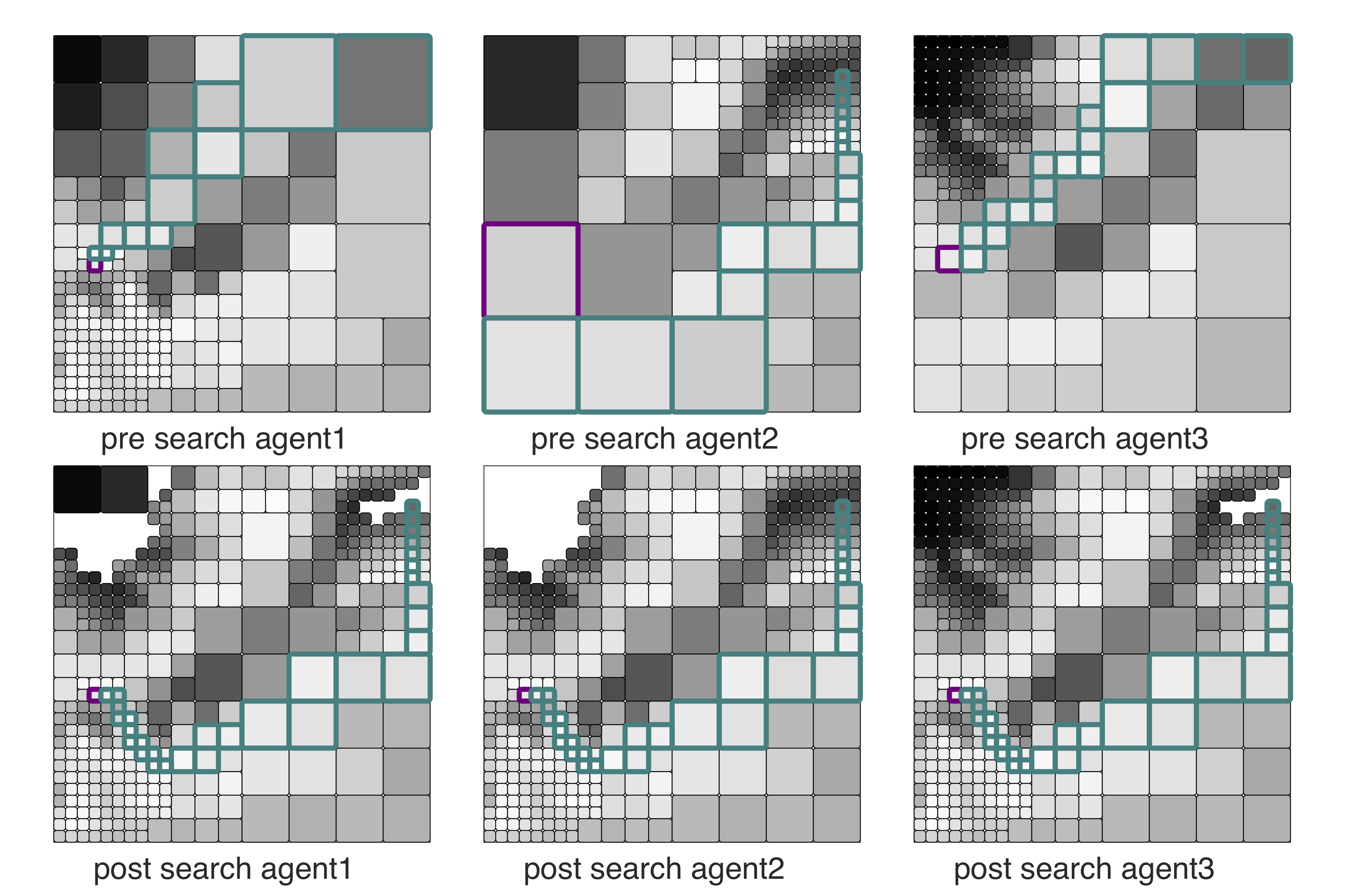
We propose a computationally efficient, hierarchical path-planning algorithm for autonomous agents (e.g., UAVs) navigating in a partially known environment W using an adaptive, discrete, cell-based approximation of W. The innovation of our approach hinges on using wavelets and beamlets to encode the district levels of fidelity (resolution) of W at different distances from the agent's current position. The motivation for this approach is simple: first, the agent's immediate reaction to an obstacle or a threat is needed only at the vicinity of its current position. Faraway obstacles or threats do not (or should not) have a large effect on the vehicle's immediate motion. Therefore, it is not prudent from a computational point of view to find a solution with great accuracy over large distances or over a long time horizon. The most accurate and reliable information of the environment is required (or it is even available) only at the vicinity of the vehicle. In that sense, the proposed algorithm can be classified under the category of "agent-centered'' search algorithm. Pictorially, such a multiresolution decomposition of the environment (say, an elevation map in this case) can be visualized as shown in the figure below.

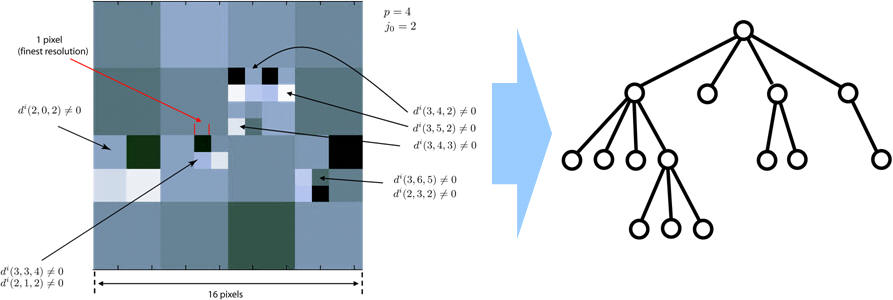
In a departure from these quadtree-based methods, in this work we make use of the wavelet transform to perform the required multiresolution decompositions of the environment. This has several advantages. First, the wavelet transform provides a very fast decomposition  of a function at different levels of resolution (the  computational complexity of the wavelet transform is of order O(n)where n is the input data. This is even better than the FFT which has complexity of order O(n log_2 n). Since the range and resolution levels can be chosen by the user, the proposed algorithm results in search graphs of known prior complexity. The algorithm is therefore scalable, and can be tailored to the available computational resources of the agent. Second, the use of wavelet transform has the added benefit of allowing the construction of the associated cell connectivity relationships directly from the wavelet coefficients, thus eliminating the need for quadtrees. Finally, the use of wavelet transform provides flexibility in terms of the choice of the wavelet basis functions, which can help in reducing the complexity of the resulting abstraction (i.e., topological search graph) of the environment.

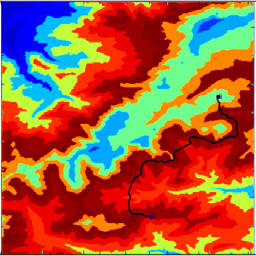
Below is an example of multiresolution path-planning.


From Wavelets to Beamlets

Wavelets induce a multiresolution hierarchy over a wide range of locations and scales. However, they exhibit a small, fixed number of preferred orientations (horizontal, vertical, diagonal), and are better described as roughly isotropic. A given path in 2D (or its approximation by a chain of line segments) has distinct, local bias towards certain orientations. Beamlets provide a framework for multiscale analysis similar to that of wavelets, in which line segments play a role analogous to the role played by points in wavelet analysis. They add two crucial elements missing from wavelet processing, however: orientation and elongation information. Beamlets are proven to achieve optimal asymptotic performance in detection problems. For instance, they have been used to design an efficient coding method for images made of curves. Beamlets are numerically more efficient than traditional curve processing algorithms, because they use the multiscale structure among them in an innovative manner.


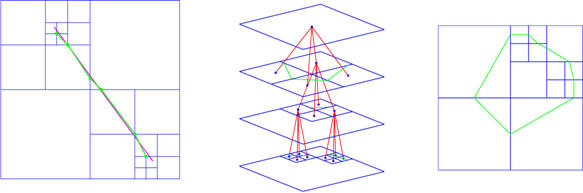
m-A* Algorithm

We propose an innovative beamlet-based graph structure for path planning that utilizes multiscale information of the environment. This information is collected via a bottom-up fusion algorithm. This new graph structure goes beyond "nearest-neighbor'' connectivity, incorporating "long-distance'' interactions between the nodes of the graph. Based on this new graph structure, we obtain a multiscale version of A*, which is advantageous when preprocessing is allowable and feasible. Compared to the benchmark A* algorithm, the use of multiscale information leads to an improvement in terms of computational complexity.

The main idea of the proposed multiscale graph structure can be summarized as follows. Consider a uniform n x n grid representing the world (or an image) assuming, without loss of generality, 4-nearest-neighbor connectivity. There are O(n^2) vertices and  O(n^2) edges in the corresponding graph. In order to reduce the number of node expansions (the most time-consuming step in all graph search algorithms), the proposed graph structure first employs a recursive dyadic partitioning to divide the environment into "blocks'' of different sizes, where the sizes are determined by the relative importance of information within those blocks. The collection of all blocks of the same size defines the information scale. The preprocessing of information within each block is conducted via an innovative Bottom-Up Fusion algorithm, which "fuses'' multiscale information from finer scales to coarser scales. Therefore, a properly designed search algorithm, defined on the preprocessed "blocks,'' can significantly reduce the number of vertices in the graph, while only slightly increasing the number of edges. As a result, path searching can be sped-up significantly, when preprocessing is feasible.

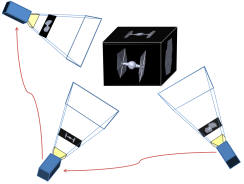
Multi-Agent Multi-Scale Path Planning

Although complete knowledge of the environment is necessary to plan an optimal solution for given task, the information about the world in which a planning agent is to plan is rarely entirely known. More likely, the agent has only a glimpse of the world abstracted away from the current state and time. This idea has led many researchers to wonder how to abstract the search space in an efficient and meaningful way. Since the early days of AI, a hierarchical abstraction of a transition system has been recognized as a crucial tool for planning in complex environments and long decision horizons.

To reduce the search space and to formulate an innate perception-action loop, we use multi-resolution graph to plan. We construct fine resolution graph near the agent to accurately represent the environment in the vicinity of the agent, and coarser resolution far-away of the agent to reduce the search space. Inevitably, this multi-resolution framework may abstract some crucial information far-away from the agent, and consequently the solution quality can degrade.

But what if our agent is allowed to use other agents' finer information and vice versa to cooperatively find a better solution? If so, what would be an efficient way to communicate the information among the agents? We try to answer these questions with a distributed search algorithm. The main idea is to communicate only the expansion result of $A^*$ to locally rewire, and hence all agents attain a common subgraph that includes a provably optimal path in the most informative graph available among all agents if one exists, without necessarily communicating the entire graph.

Sponsors

Support for this project is provided by NSF and the Army Research Lab (ARL) DCIST project.

Selected Publications



Home | People | Research | Publications | Software | Links | News | Contact