Information Theoretic Abstractions and Decision Making
Markov Decision Processes (MDP) is the standard framework for optimal sequential decision making under uncertainty. However, this framework assumes that the decision maker, customary referred to as the “agent,” is perfectly rational. That is, the agent is assumed to have unlimited computational and/or time resources to process all information and compute the optimal solution unhindered. In many practical applications this is a strong and often unrealistic assumption. For example, biological systems are adaptive in nature and excel at finding solutions to complex problems that may not be globally optimal but are “good enough” given the constraints and/or available sensory information.
With this motivation, we seek to introduce constraints (computational and otherwise) to the decision process to model agents that do not have access to unlimited resources, and hence will select actions that are not optimal in the traditional sense of maximizing value or utility, but rather in the sense of maximizing (expected) value or utility for a given processing cost. To model these scenarios, we apply a framework to develop decision-making algorithms for path-planning problems while also accounting for the information processing costs of computing these optimal solutions. More specifically, we consider information-constrained MDPs which introduce a constraint, often taken to be that of the Kullback-Leibler (KL) divergence between the posterior policy and some given prior policy, to capture the computational burden of finding optimal solutions - the more dissimilar posteriors policies are from that of the prior (in the KL sence), the more expensive they are to find. Furthermore, the introduction of the prior polices may capture, for example, the agents prior knowledge of how to accomplish a task or navigate an environment. Information-limited MDPs have connections to Information theory, and more specifically the rate distortion problem of finding optimal encoders. In addition, the framework includes a trade-off parameter which allows us to vary the degree to which the agent is resource-limited.
We apply information limited decision-making to a grid-world example where the environment is assumed to be stochastic. The world is shown in Figure 1, which is of a hierarchical nature with associated quadtree shown in Figure 2.
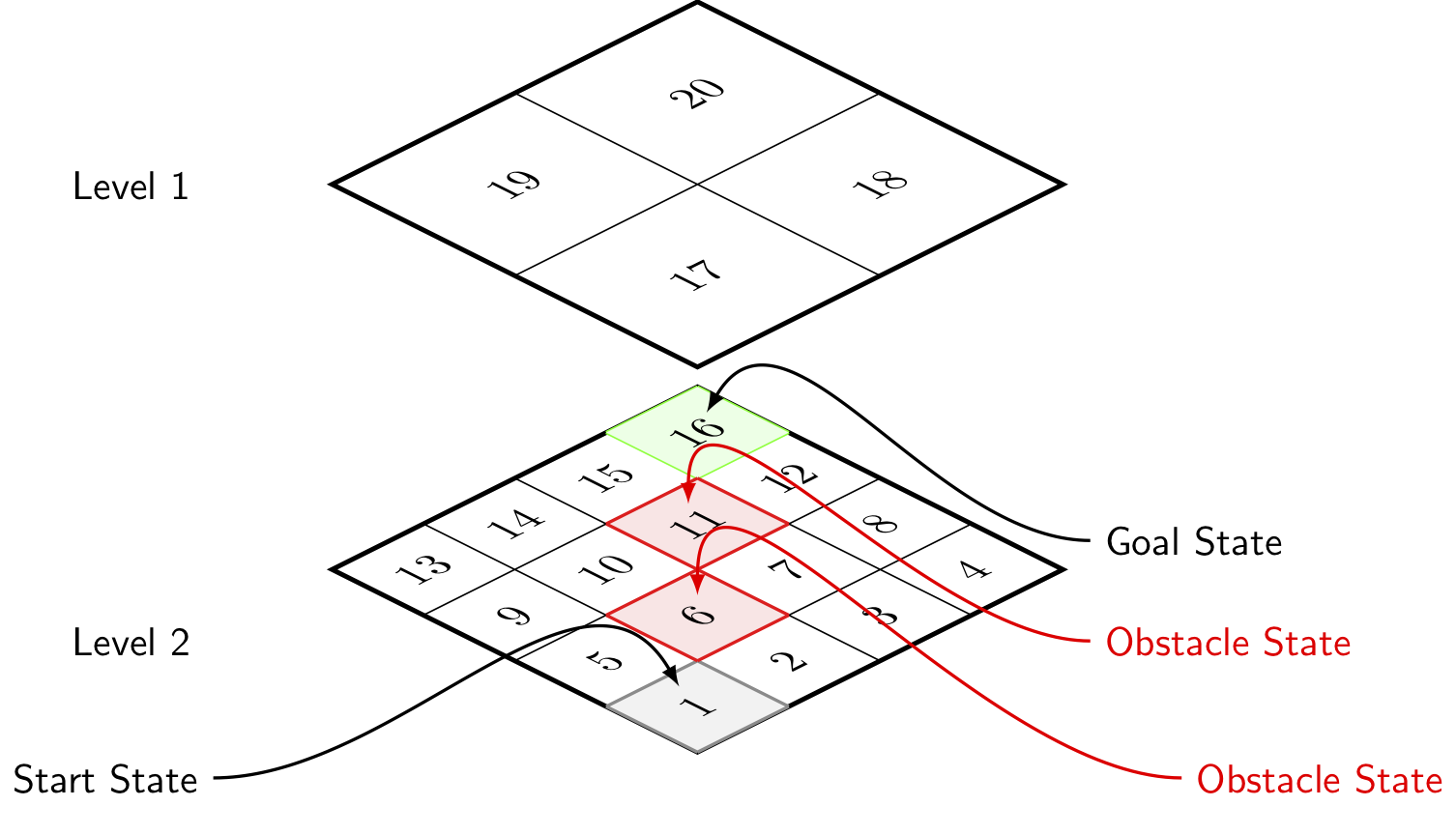
Figure 1: Grid layering with state numbering. Start state indicated in gray, obstacle states in red with goal state in green.
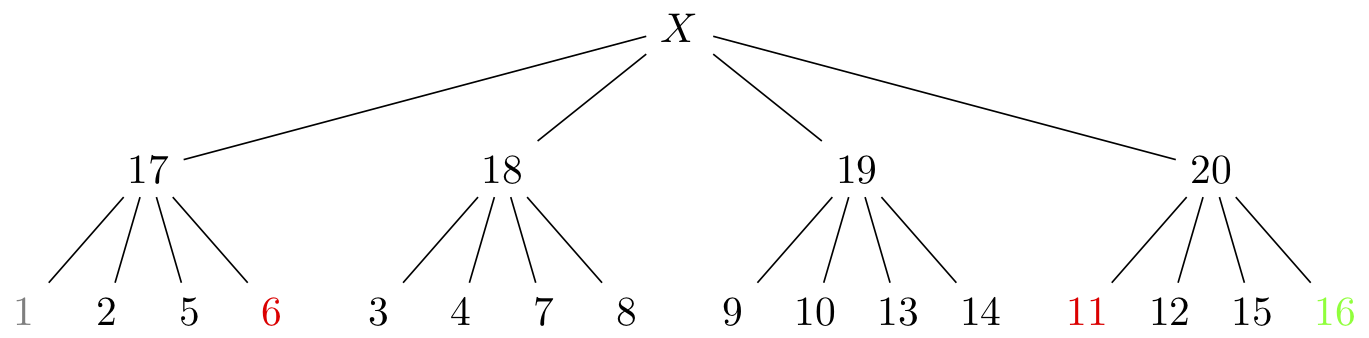
Figure 2: Hierarchical description of states with coloring consistent with description in Fig. 1.
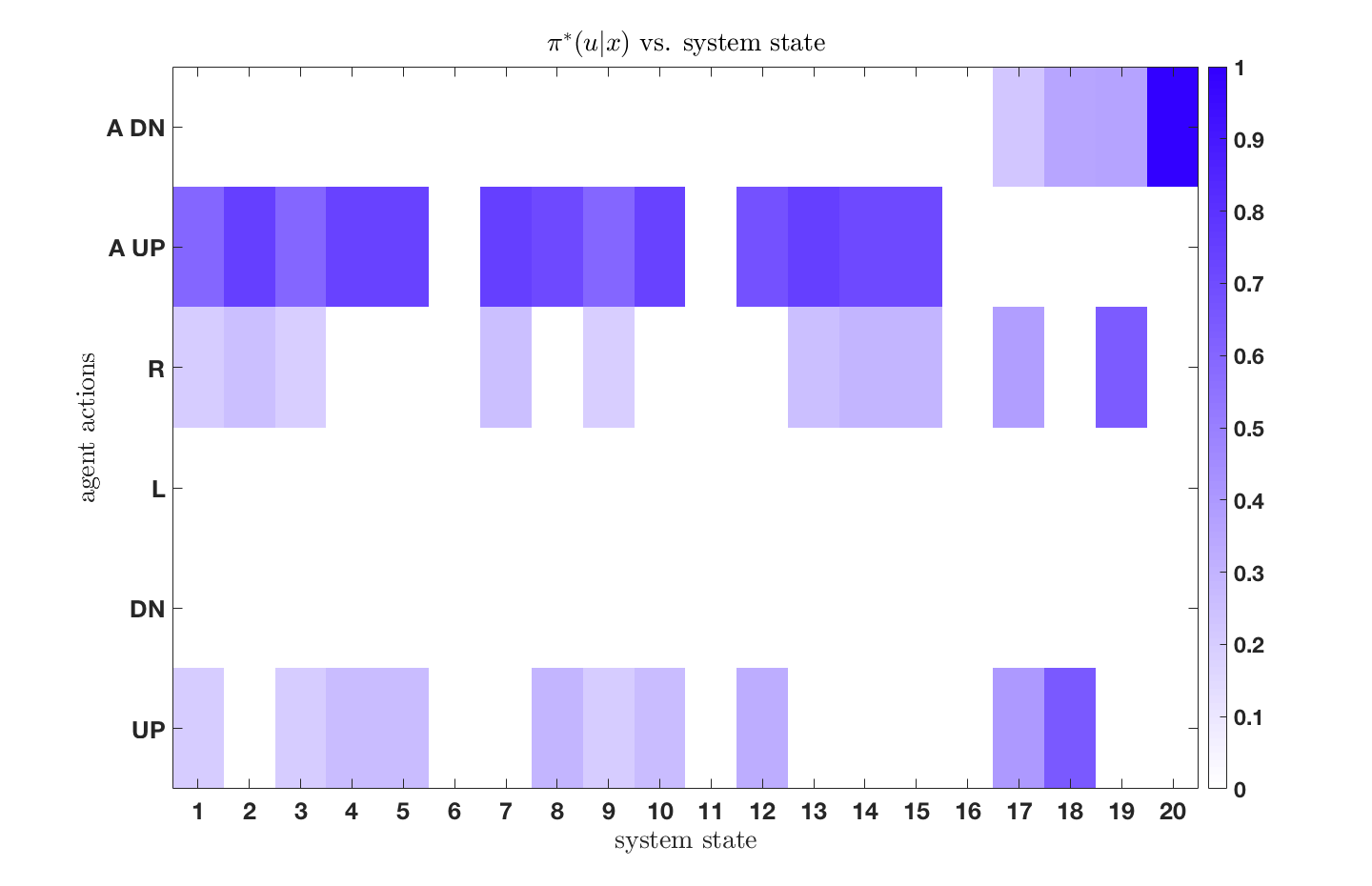
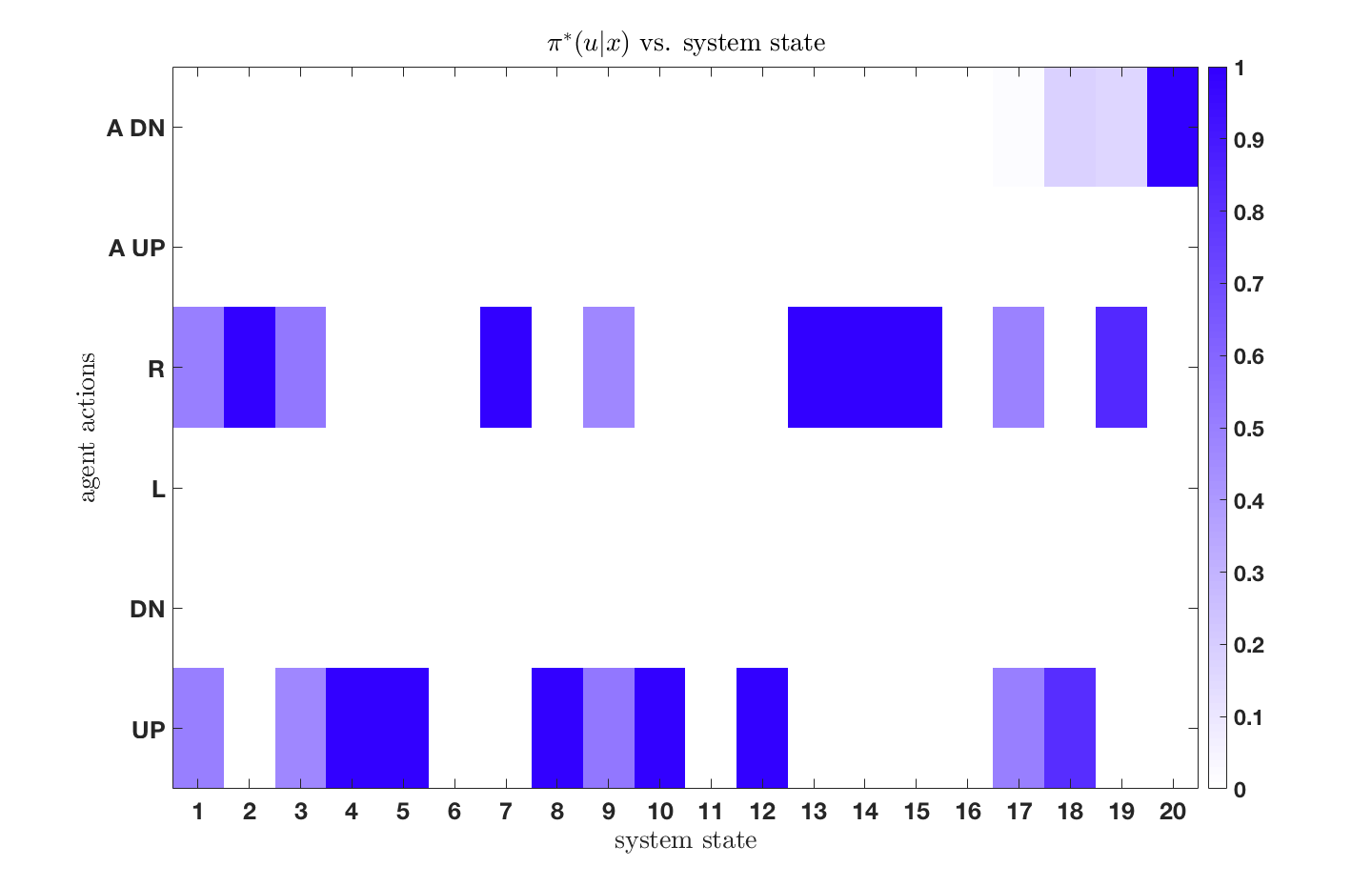
This configuration can be viewed as two environmental representations of the world, for which the agent can toggle between by utilizing a suite of sensors. Thus, the agent must not only decide the actions to take in order to navigate safely from the start to goal state, but must also decide which representation of the environment to utilize - with less detailed representation being cheaper to use.
We see that as the resource parameter is increased, indicating that the agent has more computational resources, it decides to utilize the finest-resolution sensor when navigating and aims to find a global optimally path. The agent with the lower resource parameter is, however, more resource-limited and decides to use simpler representations of the world by instead utilizing the abstractions when navigating from start to goal states. Additionally, one will find that as the resource parameter approaches infinity (rational agent), one recovers the deterministic solution to the original, unconstrained, MDP.
For more information, see our publication here.
Sponsors
This work has been sponsored by the Office of Naval Reserach (ONR) and the Army Research Lab (ARL) DCIST project.
Selected Publications
- Larsson, Daniel T., Daniel Braun, and Panagiotis Tsiotras. "Hierarchical state abstractions for decision-making problems with computational constraints." 2017 IEEE 56th Annual Conference on Decision and Control (CDC). IEEE, 2017.