Level-K Thinking for Pursuit-Evasion Games
Pursuit-Evasion Game (PEG) models a family of problems in which one group of agents attempt to track down members of another group in an environment. This type of problem has a variety of applications in military and civil fields, for example, an adversary aerial combat or a surveillance/tracking mission. Over the past decades, people strive to solve for the equilibrium of such games, either Nash equilibrium or the correlated equilibrium, where all the agents are assumed to be totally rational. However, the equilibrium is generally hard to solve and may require a significant amount of computational time.
In reality, agents (both autonomous agents and humans) only have limited computational capacity, limited information and limited time. As a result, critiques of the perfect rationality assumption in the notion of equilibrium arose, and people want to introduce the idea of bounded rationality.
To motivate this new approach to the problem, consider the classical example of “Guess 2/3 of the average”. In this game, several people guess what 2/3 of the average of their guess will be, while the number are restricted between 0 and 100. The winner is the one closest to the 2/3 of the average. The Nash equilibrium is 0, namely everyone should pick 0 as their response. However, when this game is played on a college lecture, the result deviates far from the Nash. [source: http://www.mathemafrica.org/?tag=game-theory]
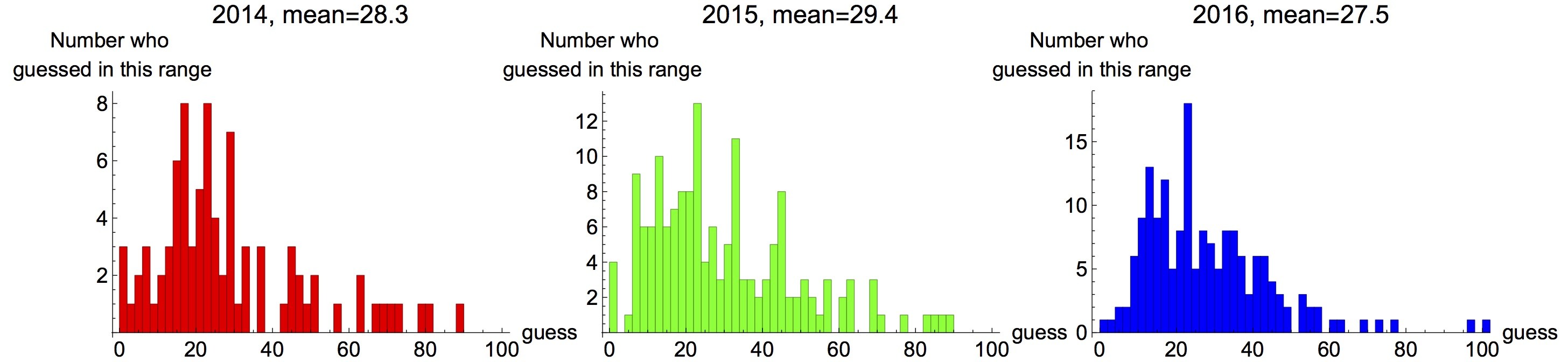
Outcome of the "Guess 2/3 of the average" game played among college students.
So, is there a possible framework, in which an agent to still find an “okay” strategy given its limited resources? In this work we use the level-k thinking to address the limited computational capacity.
In level-k framework, the level-0 agents are first defined with the most naïve strategies. Then the level-1 agents best respond to its level-0 opponents, and the level-2 agents best respond to their level-1 opponents, and so on. By adopting this framework, we can put a bound on the maximum level an agent can go for, and thus introduce the idea of bounded rationality.
We tested this framework on a discretized PEG over a 16 $\times$ 16 grid world with stochastic wind fields, as shown in the following figure.
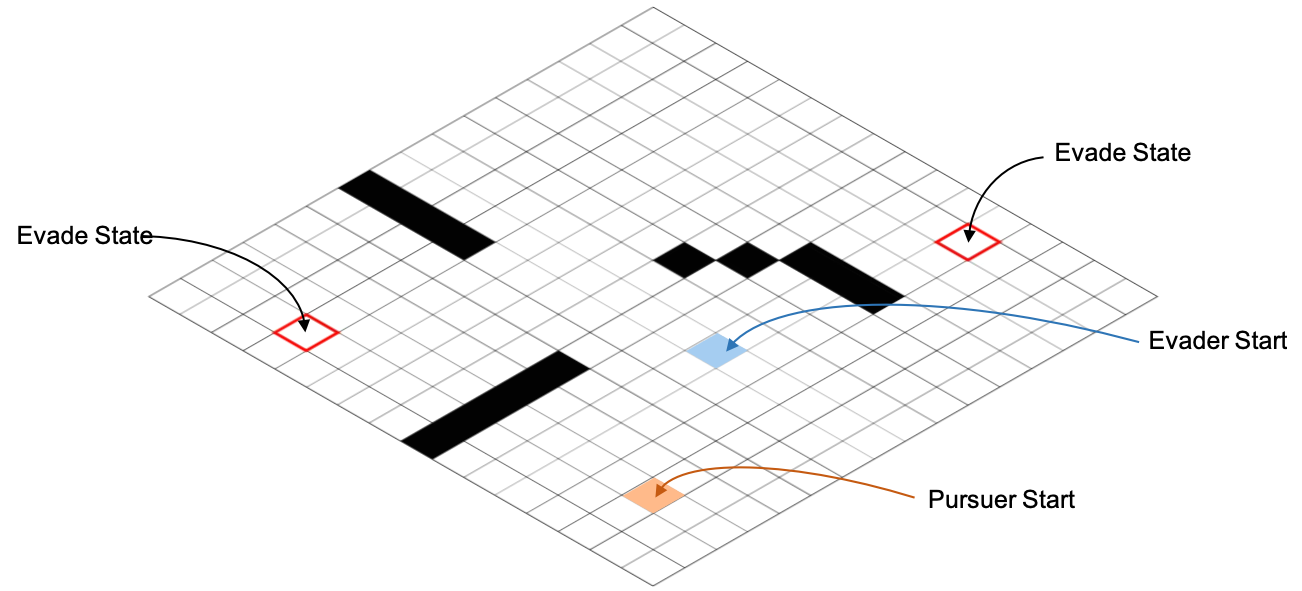
The setup of the pursuit-evasion gam.
The pursuer and the evader start at the cells marked with orange and blue respectively. An evasion is successful when the evader enters one of the two evade-states. The black cells are the obstacles, and the agent that enters these cells is considered crash and loses the game immediately.
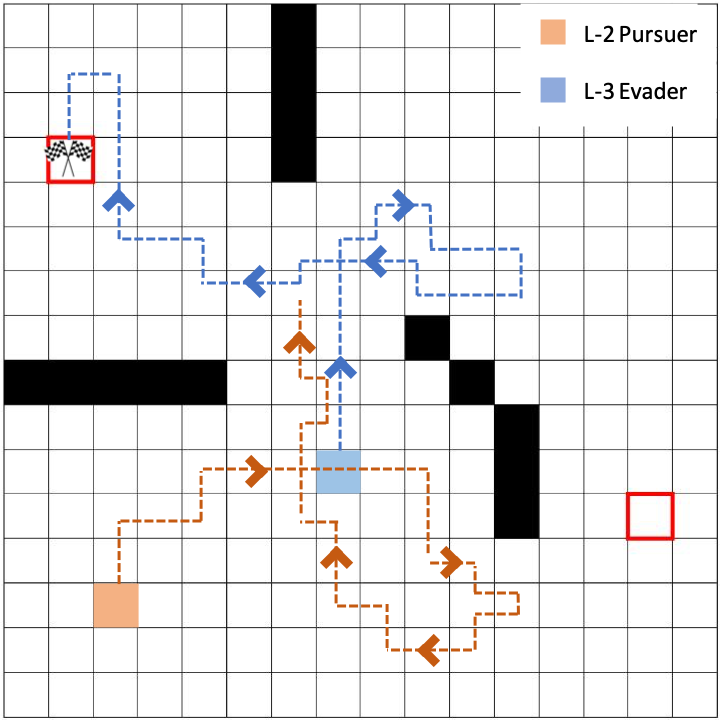
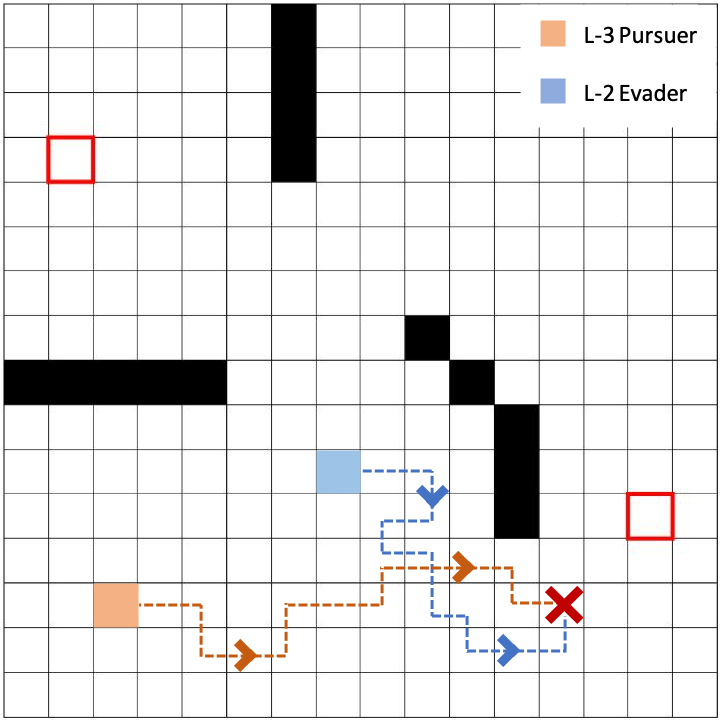
The following two sample trajectories illustrates how the level-k thinking framework works in our PEG.
The first trajectory is a level-2 pursuer against a level-3 evader, and the evader successfully evades. One can observe the "deceiving" behavior of the evader: it first heads right, which tricks the level-2 pursuer to also go right and take the short cut beneath the obstacles for defending the evade state on the right. Then, the evader suddenly turns left and go to the evade state on the left. At the time when the evader reveals that it is aiming for the other evade state, it is too late for the pursuer to capture the evader.
The second is a level-3 pursuer against a level-2 evader, and the pursuer successfully captures the evader. Different from the previous scenario, the level-3 pursuer has the perfect information about the strategies of the level-2 evader, as a result it can predict well what the evader will do in the next time step. It simply acts accordingly to maximize the probability of a successful capture.
Sponsors
This work is a part of the DCIST project and is supported by the Army Research Lab.