Optimal Strategies for Uncertain Differential Games with Applications
The major goal of this project is to develop and test ingenious solutions for controlling multiple unmanned vehicles having a common goal under the influence of external disturbances and uncertainties. The external disturbances can include winds (in the case of aerial vehicles), water currents (in the case of marine vehicles), traffic flow (in the case of self-driving cars). The difference in the actual and perceived behavior of other adversarial agents(asymmetric information)in the environment account to the uncertainties part of the research. More specifically, the project intends to find decentralized strategies for the players in a multi-player pursuit-evasion game with external disturbances and uncertainties using algorithms that are computationally efficient.
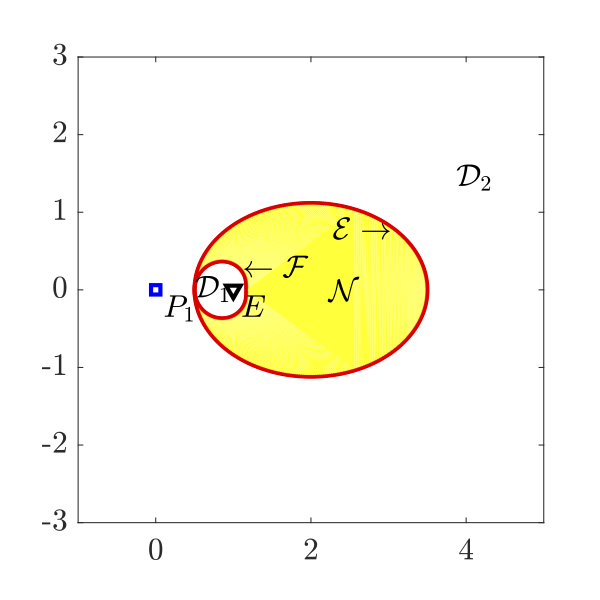
As a part of initial study, two-pursuer/single-evader pursuit-evasion problems with different information structures, assuming both pursuers to be superior to the evader in terms of their speed capabilities, and no external disturbances are examined. The time optimal evading strategies have been identified. The regions of non-degeneracy proposed in this research can be used to investigate the utility of employing two pursuers to more efficiently capture the evader. If the initial positions of the players are such that the problem is degenerate, then one of the pursuers does not play any role in the game, and the optimal evading strategy is pure evasion from the other pursuer. Optimal evading strategies against relay pursuit are also investigated by keeping one pursuer stationary.
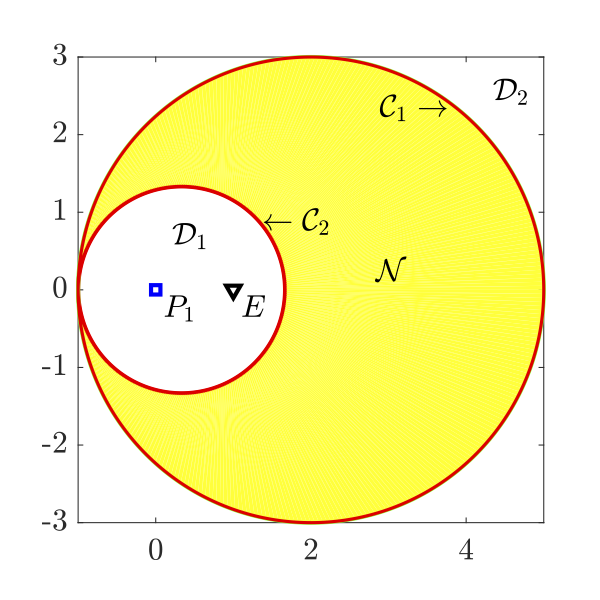
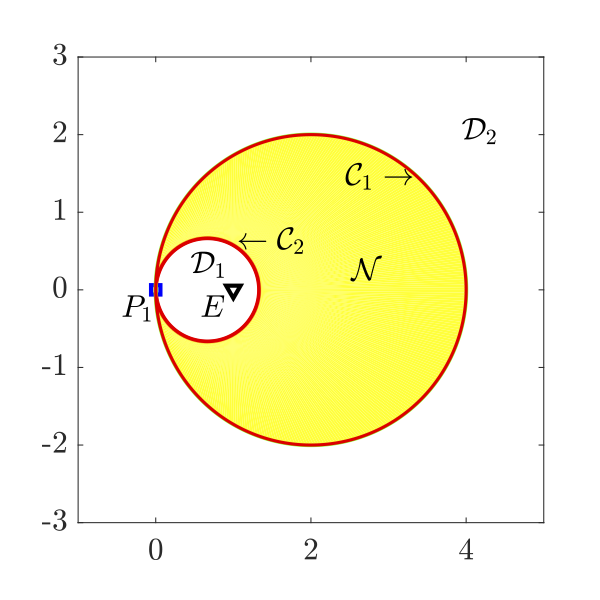
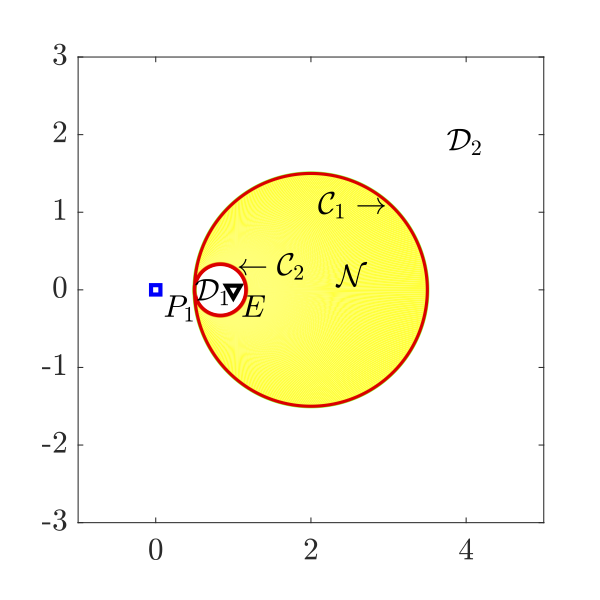
Regions of degeneracy and non-degeneracy in the case of pursuers' strategy being constant bearing

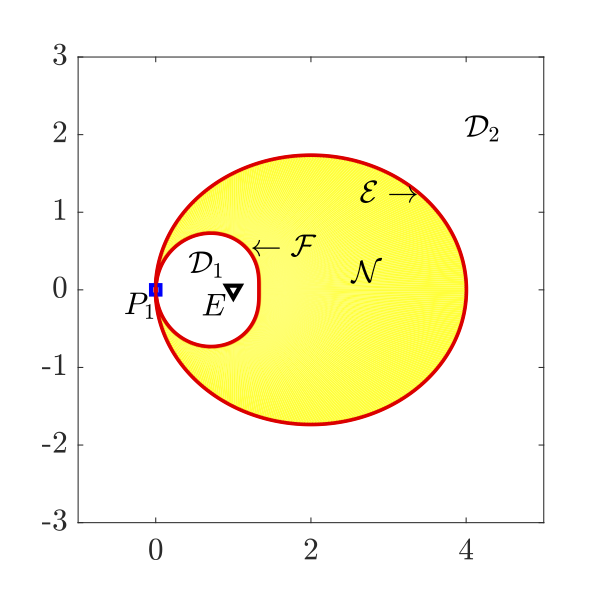
Regions of degeneracy and non-degeneracy in the case of pursuers' strategy being pure pursuit
The results of two-pursuer one-evader problems are generalized to multi-pursuer single-evader problems. It is established that the time-optimal evading strategy in both scenarios depend on the initial positions of those pursuers that captures the evader at final time. Since obtaining a closed form solution to the optimal evading strategy and the information of the corresponding pursuers that capture the evader, we propose the idea of relevance of a pursuer to the evader, based on the positions of all the players and using Apollonius circles. This approach will allow us to dynamically assign pursuers to the task of capturing the evader for any evading strategy in a smart manner. Furthermore, we use Voronoi partitions coupled with Apollonius circles to dynamically assign pursuers to various evaders, in multi-pursuer multi-evader settings, which also guarantees capture of all the evaders in finite time.
A dynamic task allocation scenario.
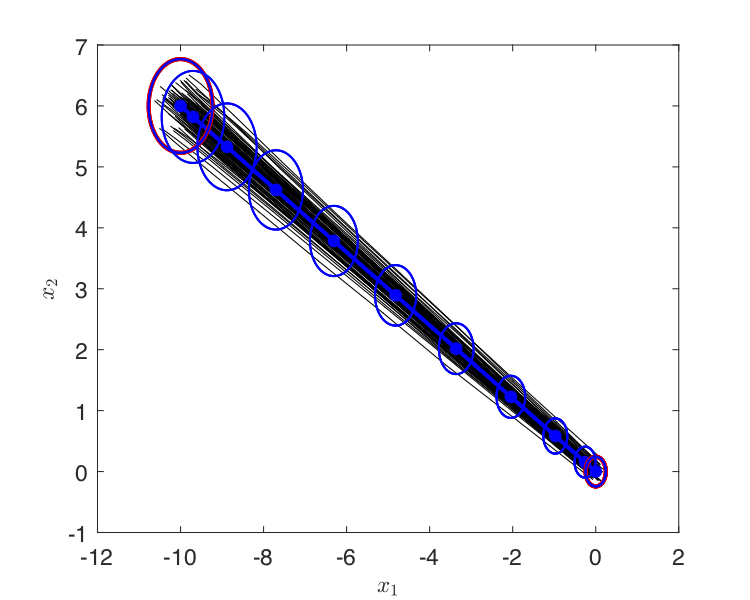
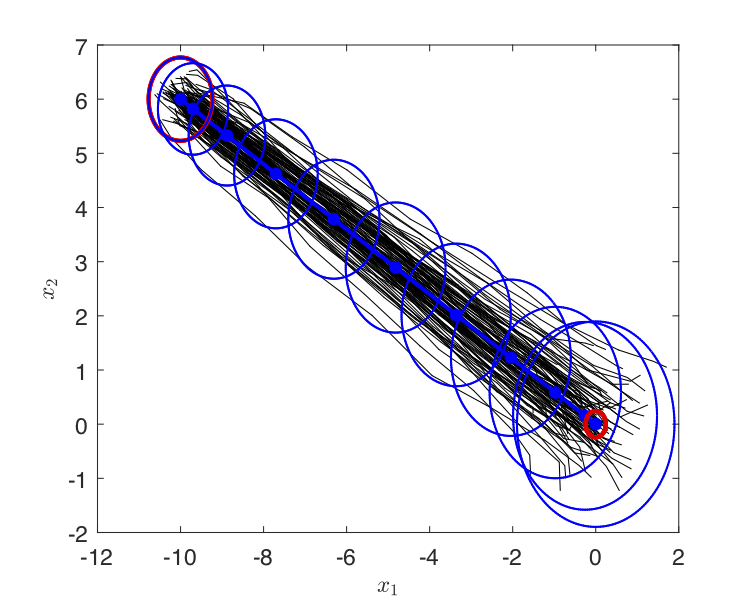
We address the problem of steering a discrete-time linear dynamical system from an initial Gaussian distribution to a final distribution in a game-theoretic setting. One of the two players strives to minimize a payoff which is quadratic while trying to meet a given mean and covariance constraint at the final time-step. The other player maximizes the payoff, but it is assumed to be indifferent to the constraint of arriving at a given terminal distribution. At first, the unconstrained version of the game is examined, and the necessary conditions for the existence of a saddle point are obtained. We then show that obtaining a solution for the one-sided constrained dynamic game is not guaranteed, and subsequently the players’ best responses are analyzed. Finally, we propose to solve the problem of steering the distribution under adversarial scenarios by converting it to a convex programming problem.
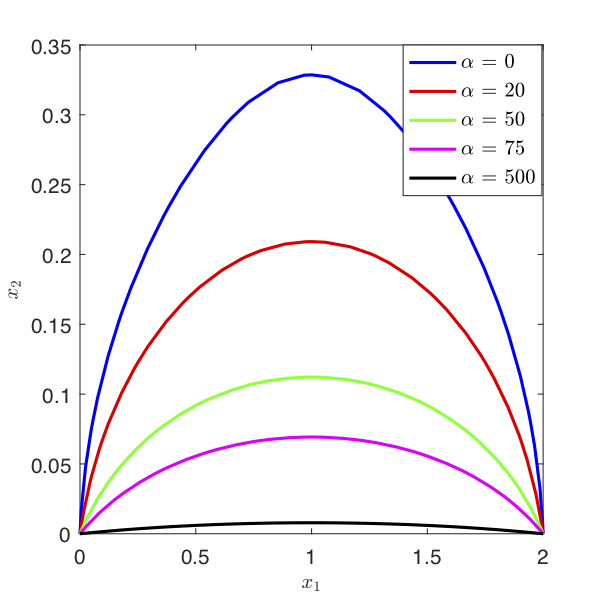
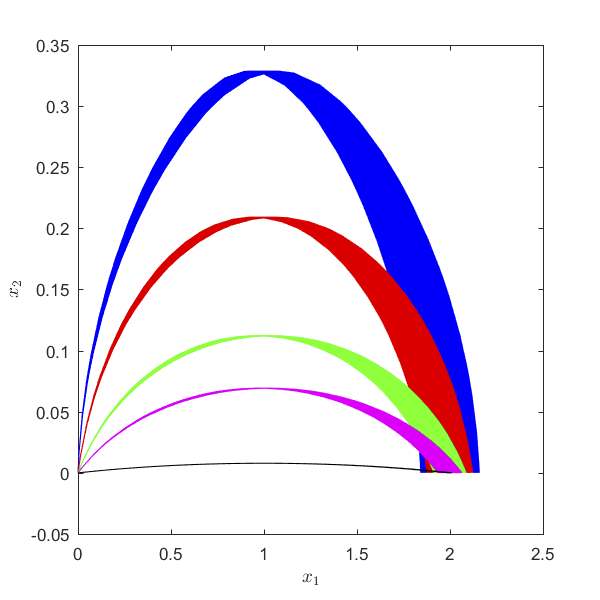
We proposed an approach to address optimal control problems with parametric uncertainties using the idea of Desensitized Optimal Control (DOC). A sensitivity function provides information about the first order variation of the state under parameter variations at a given time instant along a trajectory. It is demonstrated that the sensitivity function can be employed to effectively desensitize either an optimal trajectory or the state at a particular time instant (for example, the final state) along the optimal trajectory.
Sponsors
This project is supported by NSF.
Selected Publications
- Makkapati, V. R., Sun, W. and Tsiotras, P., "Optimal Evading Strategies for Two-Pursuer/One-Evader Problems". Journal of Guidance, Control, and Dynamics, 41(4), pp.851-862, 2018.
- Makkapati, V, R., and Tsiotras, P., Optimal Evading Strategies and Task Allocation in Multi-Player Pursuit-Evasion Problems, Dynamic Games and Applications.
- Sun, W., Tsiotras, P., and Yezzi, A., “Multiplayer Pursuit Evasion Games in 3-Dimensional Flow Fields,” Dynamic Games and Applications, (accepted February 2019). doi: 10.1007/s13235- 019-00304-4
- Exarchos, I., Theodorou, E., and Tsiotras, P., “Stochastic Differential Games - A Sampling Approach via FBSDEs,” Dynamic Games and Applications, Vol. 9, No. 2, pp. 486–505, 2019, doi:10.1007/s13235-018-0268-4
- Sun, W., Pan, Y., Theodorou, E., and Tsiotras, P., “Min-Max Differential Dynamic Programming: Continuous and Discrete Time Formulations,” AIAA Journal of Guidance, Control, and Dynamics, Vol. 41, No. 12, pp. 2568-2580, 2018, doi: 10.2514/1.G003516
- Makkapati, V. R., Dor, M., and Tsiotras, P., "Trajectory Desensitization in Optimal Control Problems," 57th IEEE Conference on Decision and Control, Miami, FL, Dec. 17–19, 2018, pp. 2478–2483. doi: 10.1109/CDC.2018.8619577
- “Optimal Strategies and Task Allocation in Multi-Pursuer Single-Evader Problems,” with V. R. Makapati, 18th International Symposium on Dynamic Games and Applications, Grenoble, France, July 9–12, 2018.
- Makkapati, V. R., Sun, W., and Tsiotras, P., "Pursuit-Evasion Problems Involving Two Pursuers and One Evader," AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, Jan. 8--12, 2018.