Bounded-Rational Decision-Making Hierarchical Models for Autonomous Agents
Information-Theoretic Abstractions and Decision making
Markov Decision Processes (MDP) is the standard framework for optimal sequential decision making under uncertainty. However, this framework assumes that the decision maker, customary referred to as the “agent,” is perfectly rational. That is, the agent is assumed to have unlimited computational and/or time resources to process all information and compute the optimal solution unhindered. In many practical applications this is a strong and often unrealistic assumption. For example, biological systems are adaptive in nature and excel at finding solutions to complex problems that may not be globally optimal but are “good enough” given the constraints and/or available sensory information.
With this motivation, we seek to introduce constraints (computational and otherwise) to the decision process to model agents that do not have access to unlimited resources, and hence will select actions that are not optimal in the traditional sense of maximizing value or utility, but rather in the sense of maximizing (expected) value or utility for a given processing cost. To model these scenarios, we apply a framework to develop decision-making algorithms for path-planning problems while also accounting for the information processing costs of computing these optimal solutions. More specifically, we consider information-constrained MDPs which introduce a constraint, often taken to be that of the Kullback-Leibler (KL) divergence between the posterior policy and some given prior policy, to capture the computational burden of finding optimal solutions - the more dissimilar posteriors policies are from that of the prior (in the KL sence), the more expensive they are to find. Furthermore, the introduction of the prior polices may capture, for example, the agents prior knowledge of how to accomplish a task or navigate an environment. Information-limited MDPs have connections to Information theory, and more specifically the rate distortion problem of finding optimal encoders. In addition, the framework includes a trade-off parameter which allows us to vary the degree to which the agent is resource-limited.
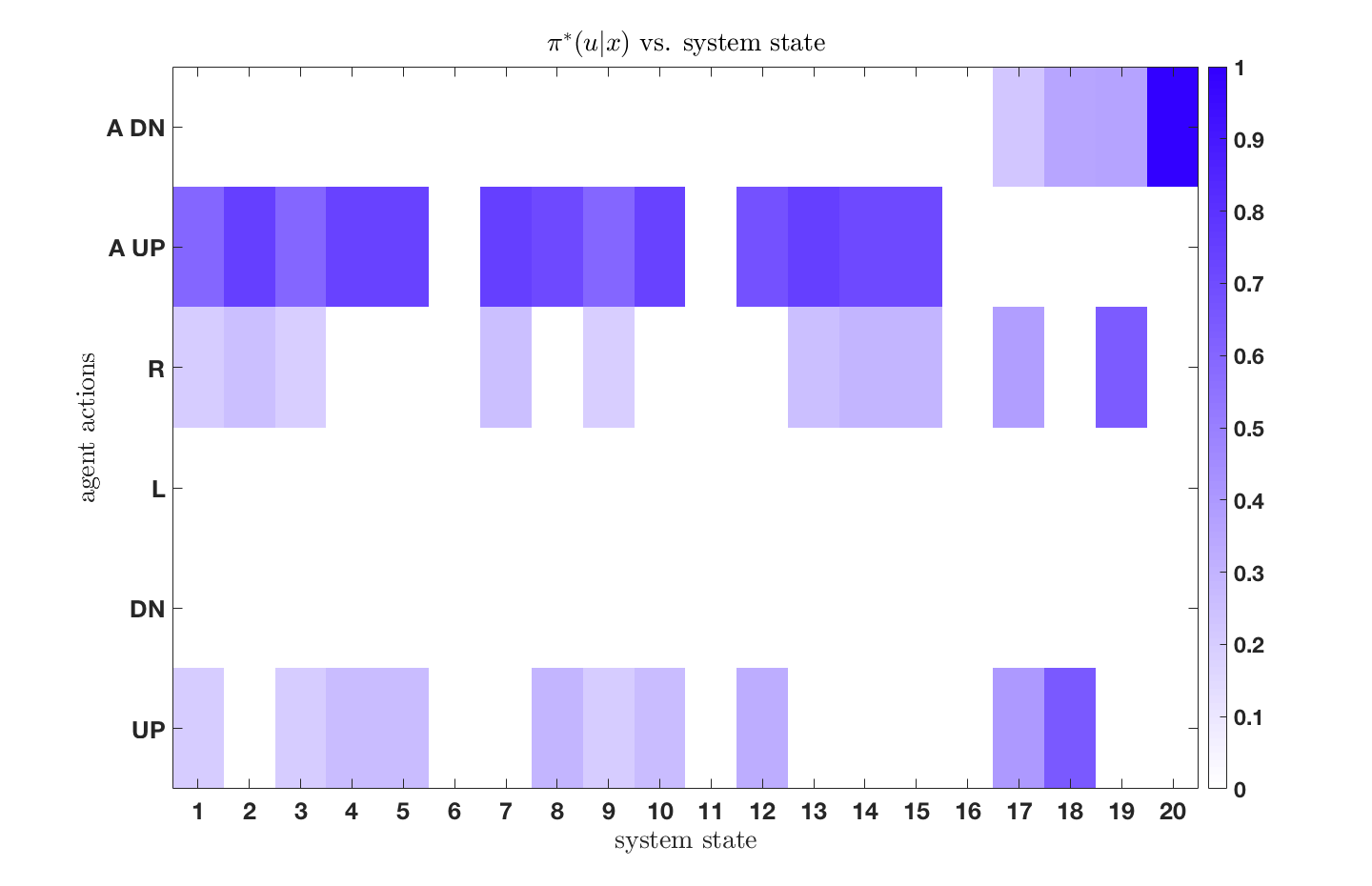
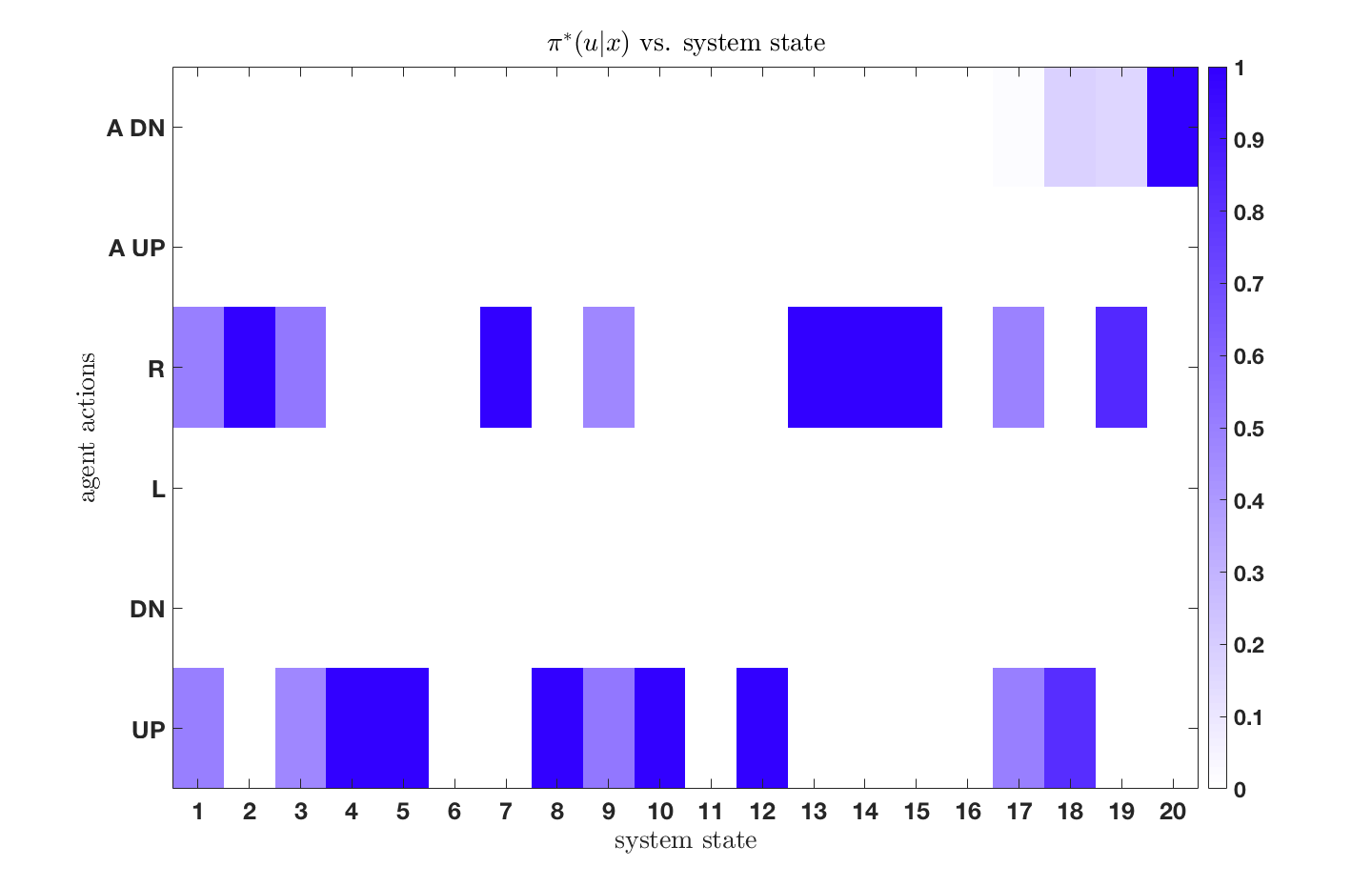
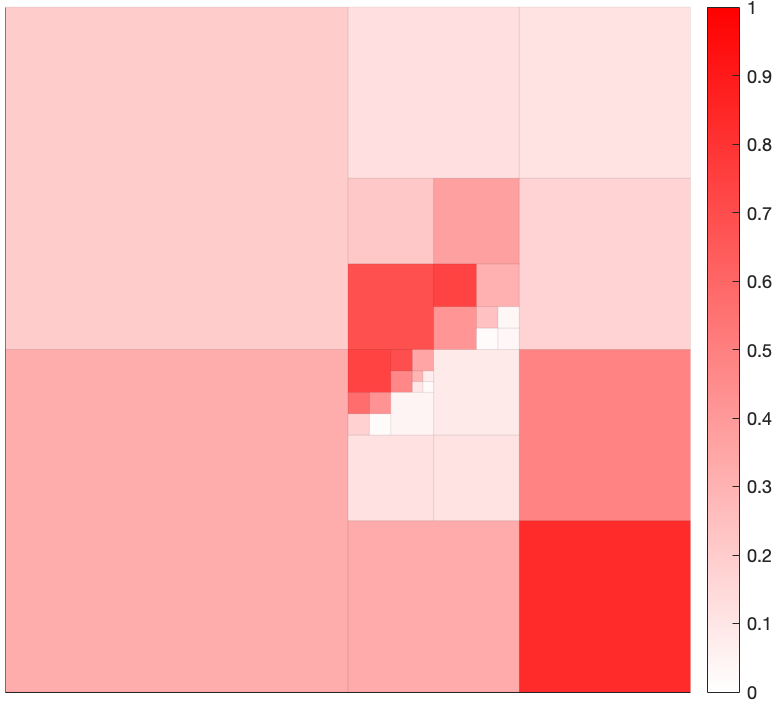
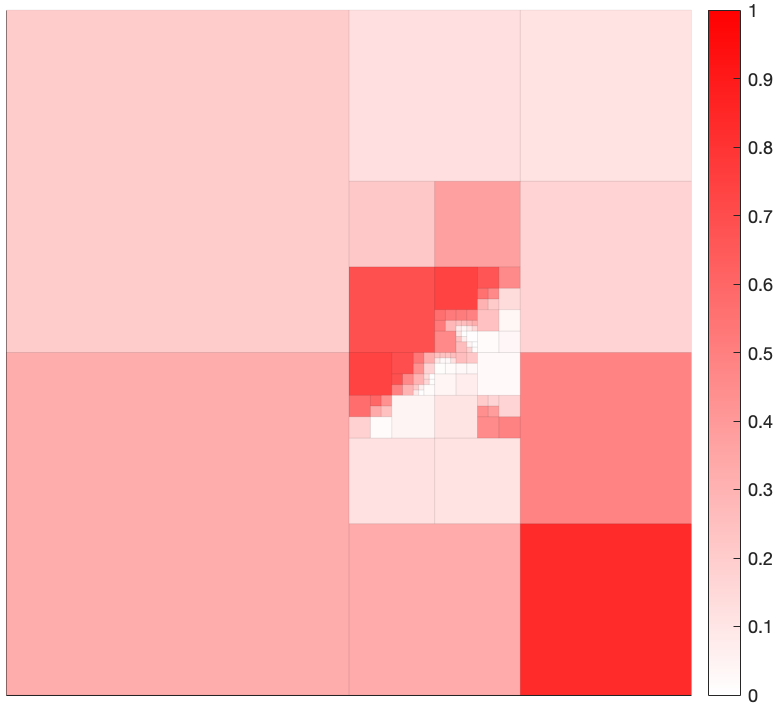
We apply information limited decision-making to a grid-world example where the environment is assumed to be stochastic. The world is shown in Figure 1, which is of a hierarchical nature with associated quadtree shown in Figure 2.
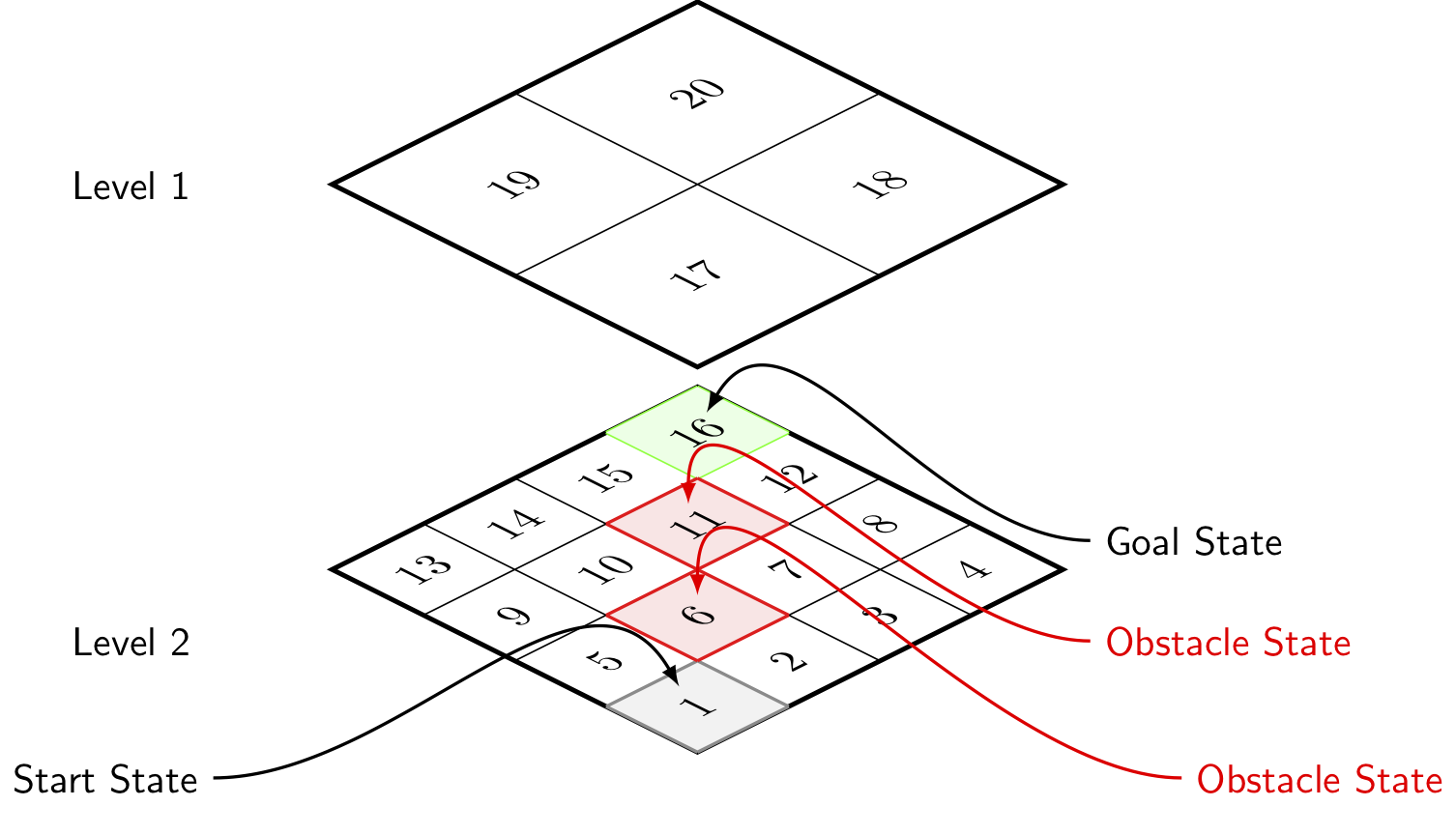
Figure 1: Grid layering with state numbering. Start state indicated in gray, obstacle states in red with goal state in green.
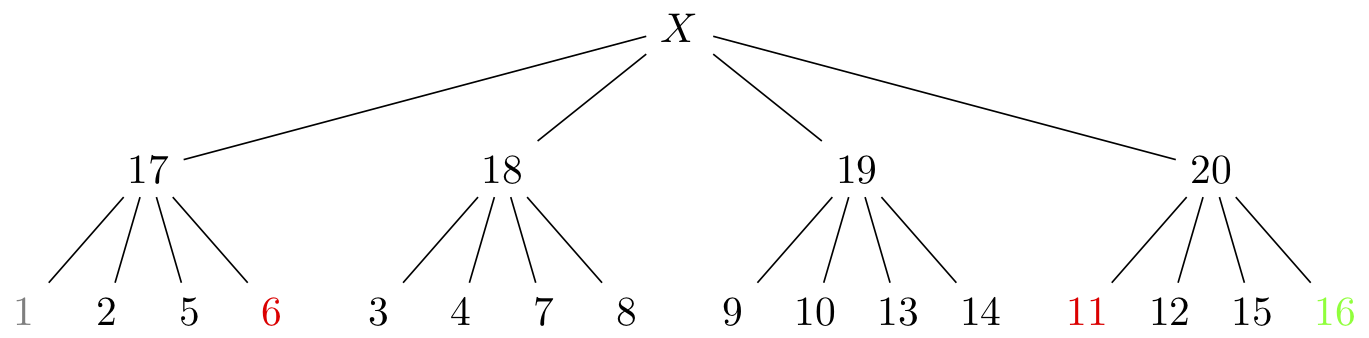
Figure 2: Hierarchical description of states with coloring consistent with description in Fig. 1.
This configuration can be viewed as two environmental representations of the world, for which the agent can toggle between by utilizing a suite of sensors. Thus, the agent must not only decide the actions to take in order to navigate safely from the start to goal state, but must also decide which representation of the environment to utilize - with less detailed representation being cheaper to use.
We see that as the resource parameter is increased, indicating that the agent has more computational resources, it decides to utilize the finest-resolution sensor when navigating and aims to find a global optimally path. The agent with the lower resource parameter is, however, more resource-limited and decides to use simpler representations of the world by instead utilizing the abstractions when navigating from start to goal states. Additionally, one will find that as the resource parameter approaches infinity (rational agent), one recovers the deterministic solution to the original, unconstrained, MDP.
For more information, see our publication here.
Hierarchical Abstractions for Agents with Computational Limitations
Information theory provides a principled framework for obtaining optimal compressed representations of a signal. The ability to form such compressed representations, also known as abstractions, has widespread uses in many fields, ranging from signal processing and data transmission, to robotic motion planning in complex environments, and many others. Particularly for autonomous systems, simplified representations of the environment which the agent operates in are preferred, as they decrease the on-board memory requirements and reduce the computational time required to find feasible or optimal solutions for planning.
The drawback of previous works is that they do not directly address the generation of the abstractions, and instead rely on them to be either provided a-priori or created in a manner that is known beforehand. Furthermore, existing works do not consider the computational limitations of the agent. That is, existing works do not consider in their formulation that agents with limited on-board resources may not employ the same representation, or depiction, of the environment as agents that are not resource limited. Thus, existing approaches do not model a resource-limited agent who is not able to process all data collected by observing its surroundings due to its computational limitations, leading to the need for simplification of the space in which it operates.
We address the issue of abstraction generation for a given environment, and formulate a novel optimization problem that leverages concepts from information theory to obtain representations of an environment that are a function of the agent's available resources, when the environment is represented as a multi-resolution quadtree. Two algorithms are proposed to solve the resulting optimization problem with theoretical guarantees of our proposed approach presented and discussed.
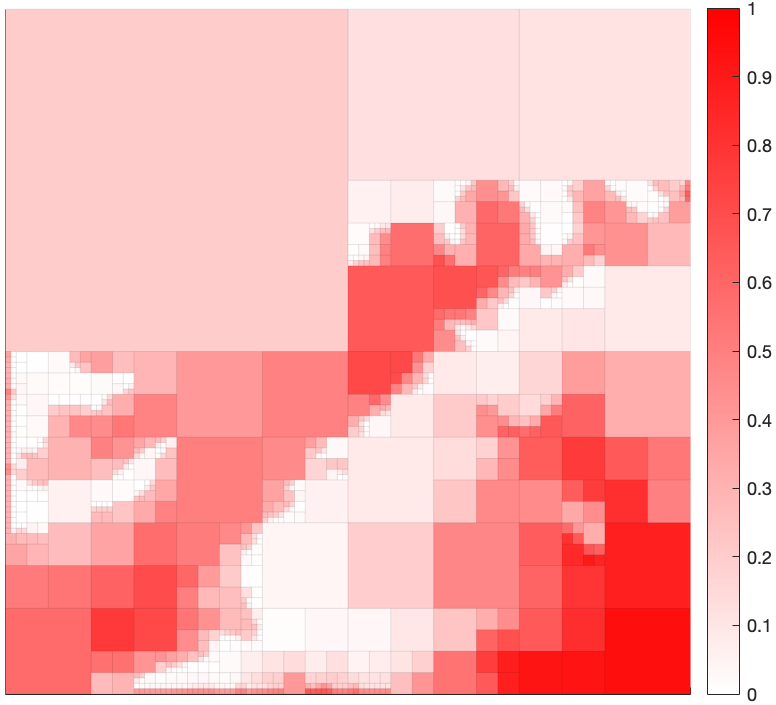
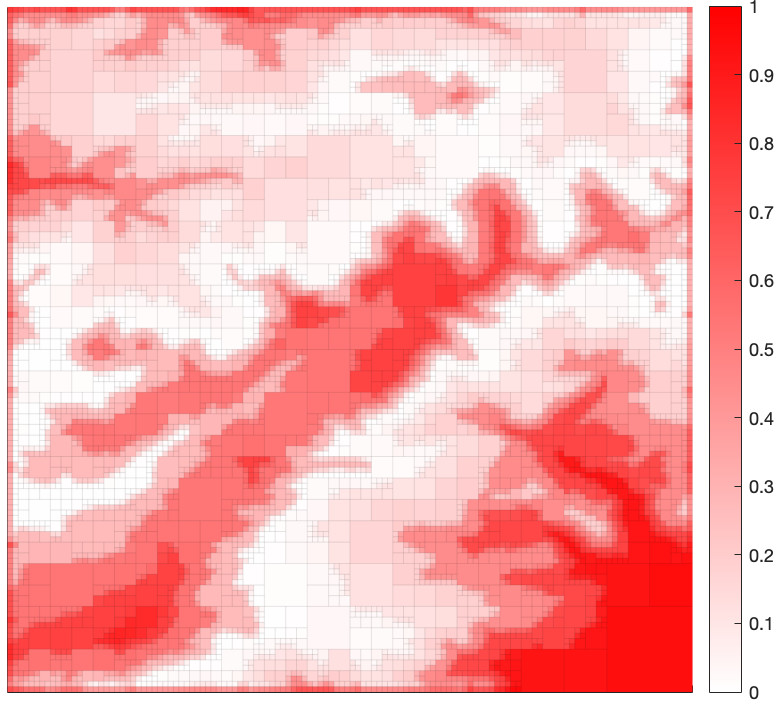
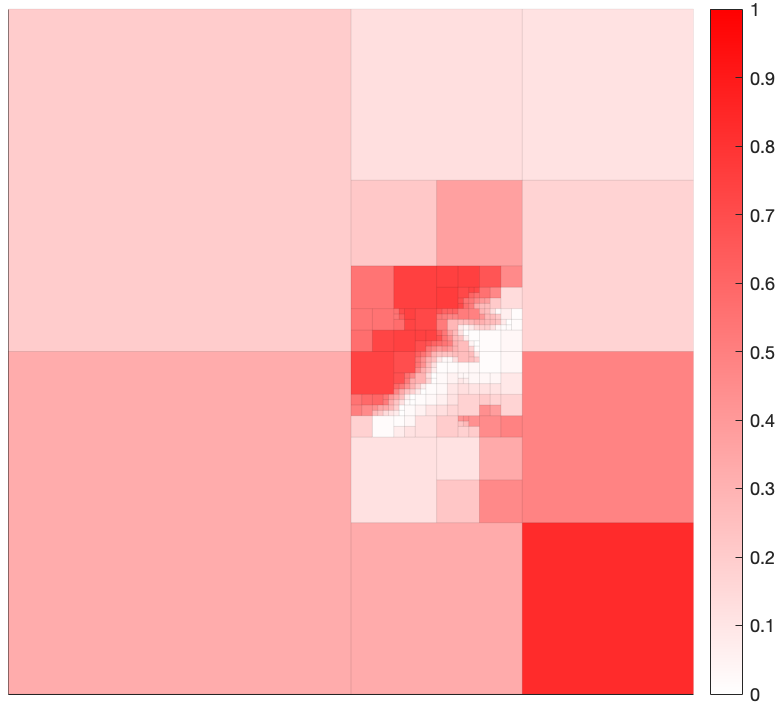
We present a numerical example to demonstrate the emergence of abstractions in a grid-world setting by ing the environment shown in Figure 4, which has dimension 128$\times$128. We view this map as representing an environment where the intensity of the color indicates the probability that a given cell is occupied. In this view, the map in Figure 4 can be thought of as an occupancy grid (OG) where the original space is considered to be the elementary cells shown in the figure.
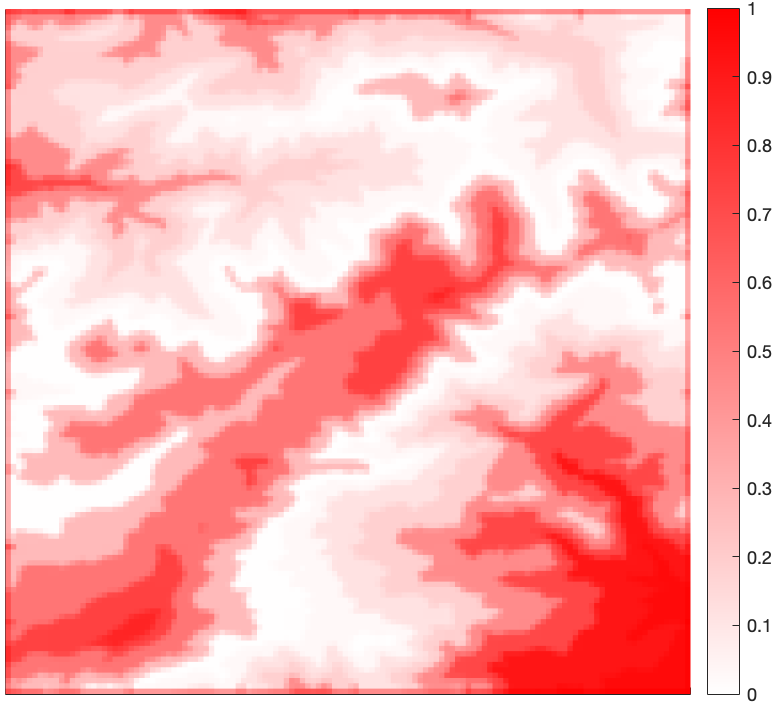
Figure 4: 128$\times$128 original map of environment. Shading of red indicates the probability that a cell is occupied.
Region-Agnostic Abstraction
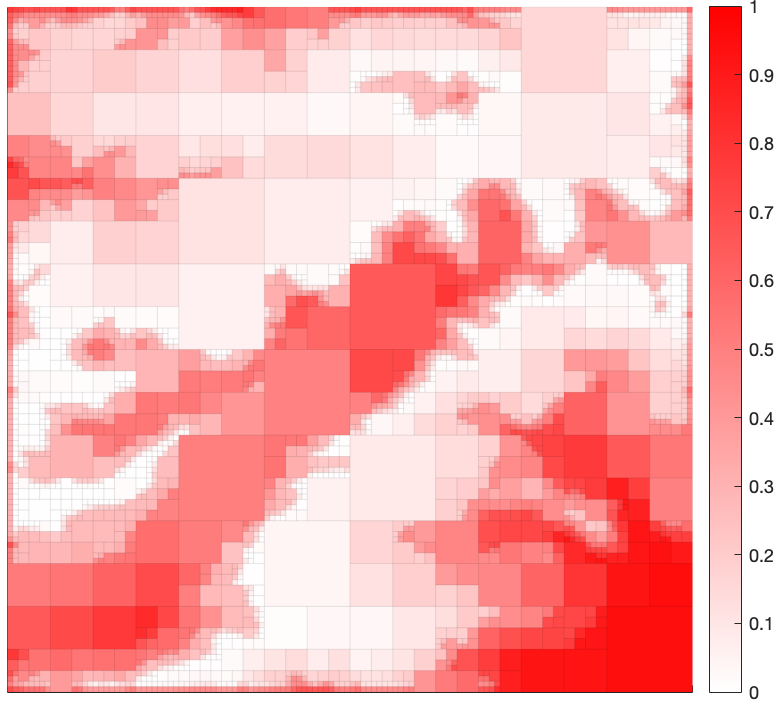
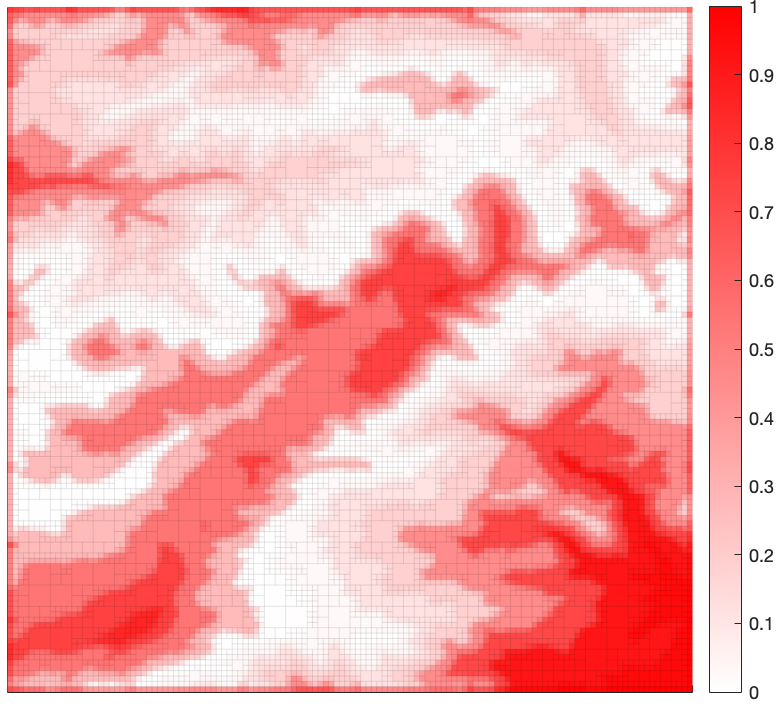
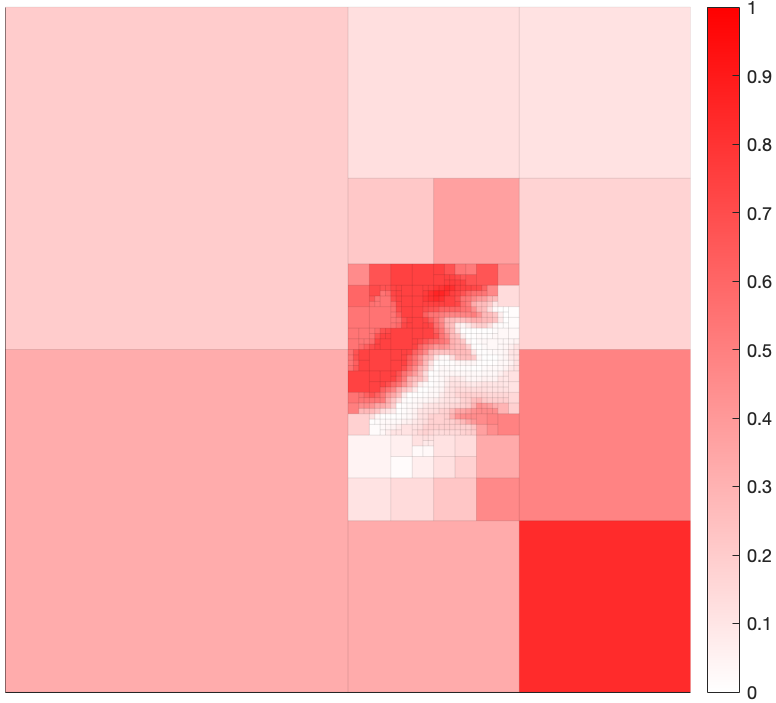
We wish to compress the original environment to an abstract representation in the form of a quadtree, while preserving as much information regarding cell occupancy as possible. The abstractions emerge as a function of a non-negative trade-off parameter $\beta > 0$, which balances the amount of compression versus the amount of relevant information retained in the abstract representation (quadtree). Environment depictions for various values of $\beta$ are shown in Figures 5-8. As seen in these figures, the solution returned by the algorithm approaches that of the original space as $\beta \to \infty$, with a spectrum of solutions obtained as $\beta$ is varied. These figures show that areas containing high relevant information content are refined first while leaving the regions with less information content to be refined at a higher $\beta$.
Region-Specific Abstraction
In addition, we are able to obtain region-specific abstractions without modification to our framework or proposed algorithms. This is possible by introducing a non-uniform $p(x)$ distribution, where the information-theoretic framework utilizes $p(x,y) = p(y|x)p(x)$.
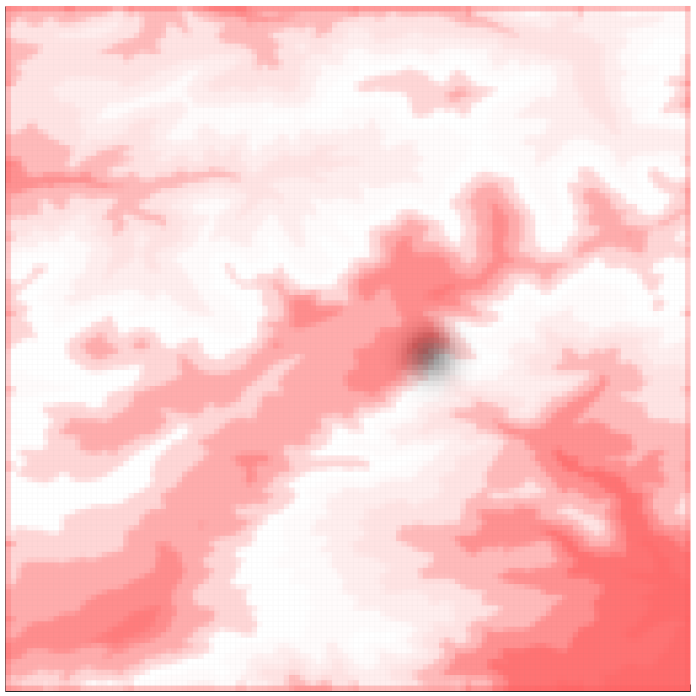
Figure 9: 128$\times$128 original map of environment with overlayed $p(x)$.
To demonstrate this, we introduce a non-uniform $p(x)$ to the environment in Figure 4, shown in Figure 9. Visualizations of the resulting solutions obtained from the algorithm are provided in Figures 10-13. These figures show that the algorithm refines only regions for which $p(x) > 0$ and that the refinement is progressive, increasing as $\beta \to \infty$.
As in the region-agnostic case, $\beta$ resembles a sort of a ``gain" that can be increased, resulting in progressively more informative solutions of higher cardinality. Thus, once the map is given, changing only the value of $\beta$ gives rise to a variety of solutions of varying resolution.
The importance of this work lies in the development of a framework that allows for the emergence of abstractions in a principled manner, requiring only the specification of a relevant variable that contains the information we wish to retain in the resulting compressed representation. The framework then searches for trees that not only compress the original space, but maximally preserve the information regarding the relevant variable. The results can be utilized in decision-making problems to systematically compress the given state representation or in path-planning algorithms to develop reduced complexity representations of the original planning space. In addition, we can view $\beta$ as a "rationality parameter," where agents with low $\beta$ are considered to be more resource limited, thus utilizing simpler, lower cardinality, representations of the environment.
For more information, see our publication here.
Path-Planning for Agents with Computational Constraints
Path and motion planning for autonomous systems has long been an area of research within the robotics and artificial intelligence communities. This has led to the development of a number of frameworks which formulate planning tasks in terms of mathematical optimization problems, which can then be solved by utilizing approaches from optimization theory and optimal control. However, planning in complex domains can be a challenging problem, and requires the agents to spend time and computational resources in order to find solutions, leading to an intrinsic need to balance computational complexity and optimality.
We consider the problem of complexity reduction for path-planning for autonomous agents. Specifically, our goal is to construct a path-planning problem that incorporates time and computational constraints faced by the agent directly in the formulation. To accomplish this, we utilize concepts from information theory and state-aggregation in AI to form task-specific abstractions of a given environment without the need to specify its structure a-priori. The developed framework provides for connections between anytime algorithms, information-theoretic compression, path-planning and bounded rationality.
Our framework assumes that there exists an integer $\ell > 0$ such that the environment is contained within a hypercube of side length $2^\ell$ and that the environmental abstractions are of the form of multi-resolution quadtrees, although our approach is generalizable to any tree structure. Our objective is then to select among feasible quadtrees as a function of agent capability so as to reduce the computational complexity of path-planning. Figure 14 shows the interplay between quadtree (hierarchical) representations and the associated spacial (graphical) representation utilized for planning. Each tree representation of an environment has an associated graph, which can be utilized for planning.


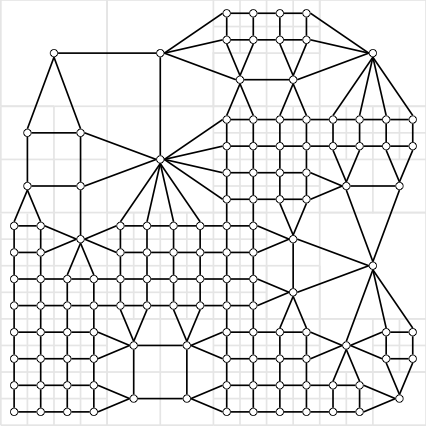
Figure 14: Tree representation (top), corresponding grid depiction (left) and associated graph (right) for a $2^{\ell} \times 2^{\ell}$ with $\ell = 4$ environment.
We are interested in reducing the complexity of path-planning problems by utilizing information-theoretic principles to select the tree on which the path is planned as a function of the agent's available resources. We assume a start node and goal node are provided, along with an occupancy grid of the environment. Since our framework utilizes the flexibility of occupancy grids, which encode obstacle information probabilistically, we define feasibility in terms of a parameter $\varepsilon \in [0,1]$, with lower values of $\varepsilon$ leading to a more conservative agents. In addition, our formulation incorporates path-feasibility directly into the cost function, allowing an autonomous agent to deduce path feasibility from knowledge of only path cost.
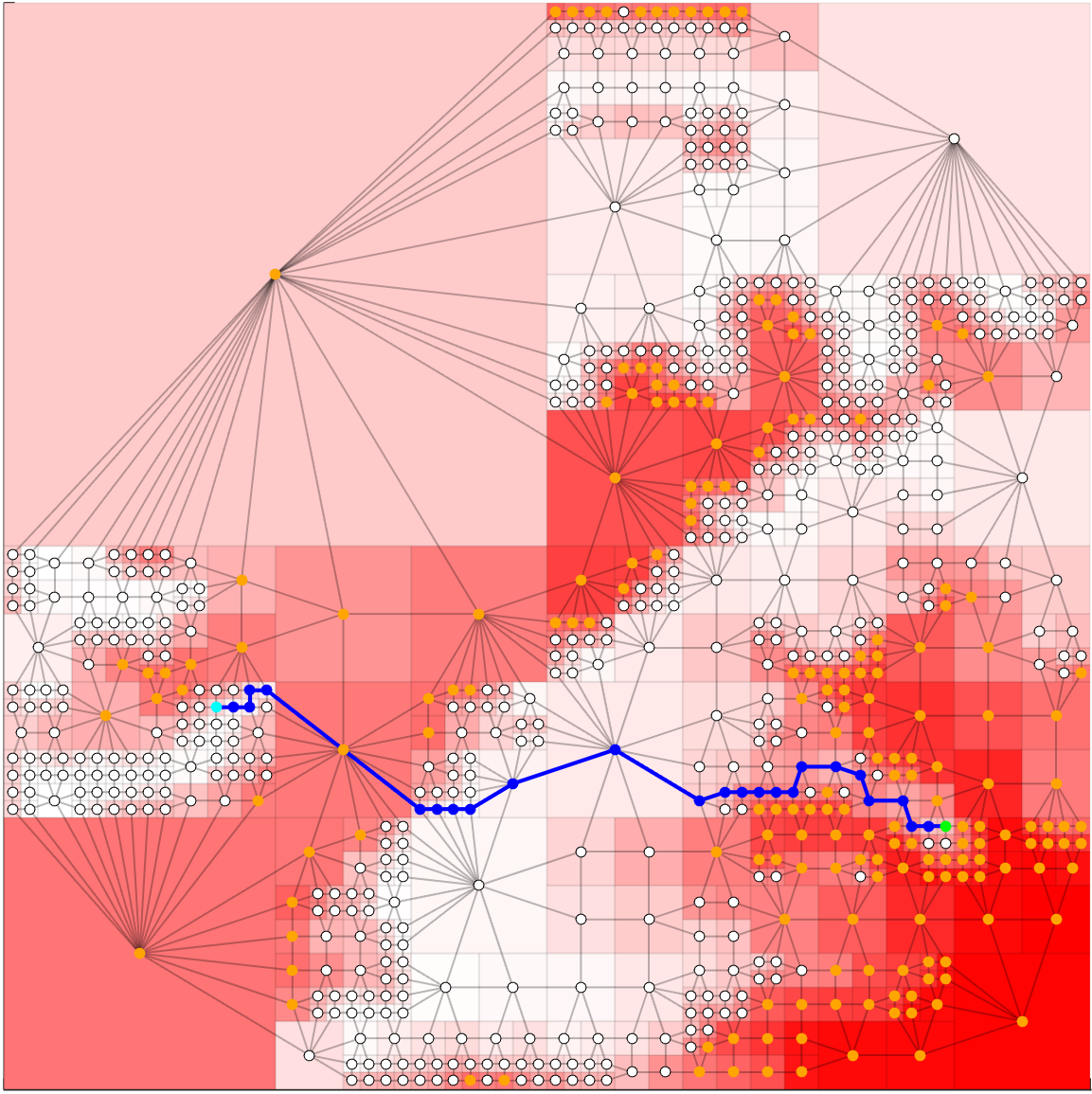
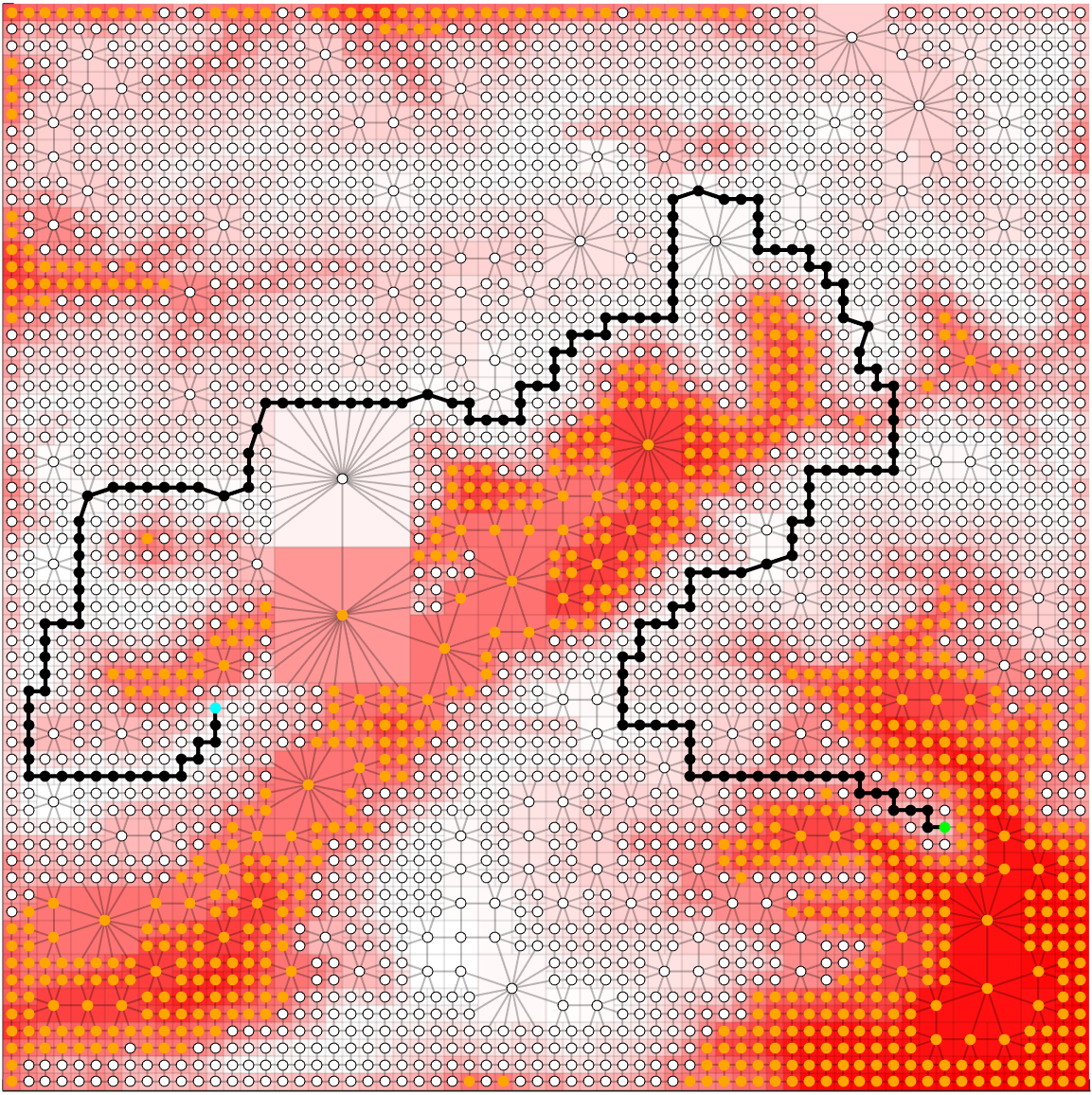
We utilize the framework presented here to obtain the quadtree representation of the environment as a function of a trade-off parameter representing the agent capabilities. Given a sequence of trees, each tree correspoding to a specific setting of the trade-off parameter $\beta > 0$, we then plan a path on each of the associated graphs, leading to a corresponding sequence of paths. In addition, our formulation of the problem guarantees that the objective function value of the paths decrease monotonically as the resolution of the environment increases. We demonstrate our approach on a $64 \times 64$ occupancy grid, as shown in Figure 15 along with an associated finest resolution path.
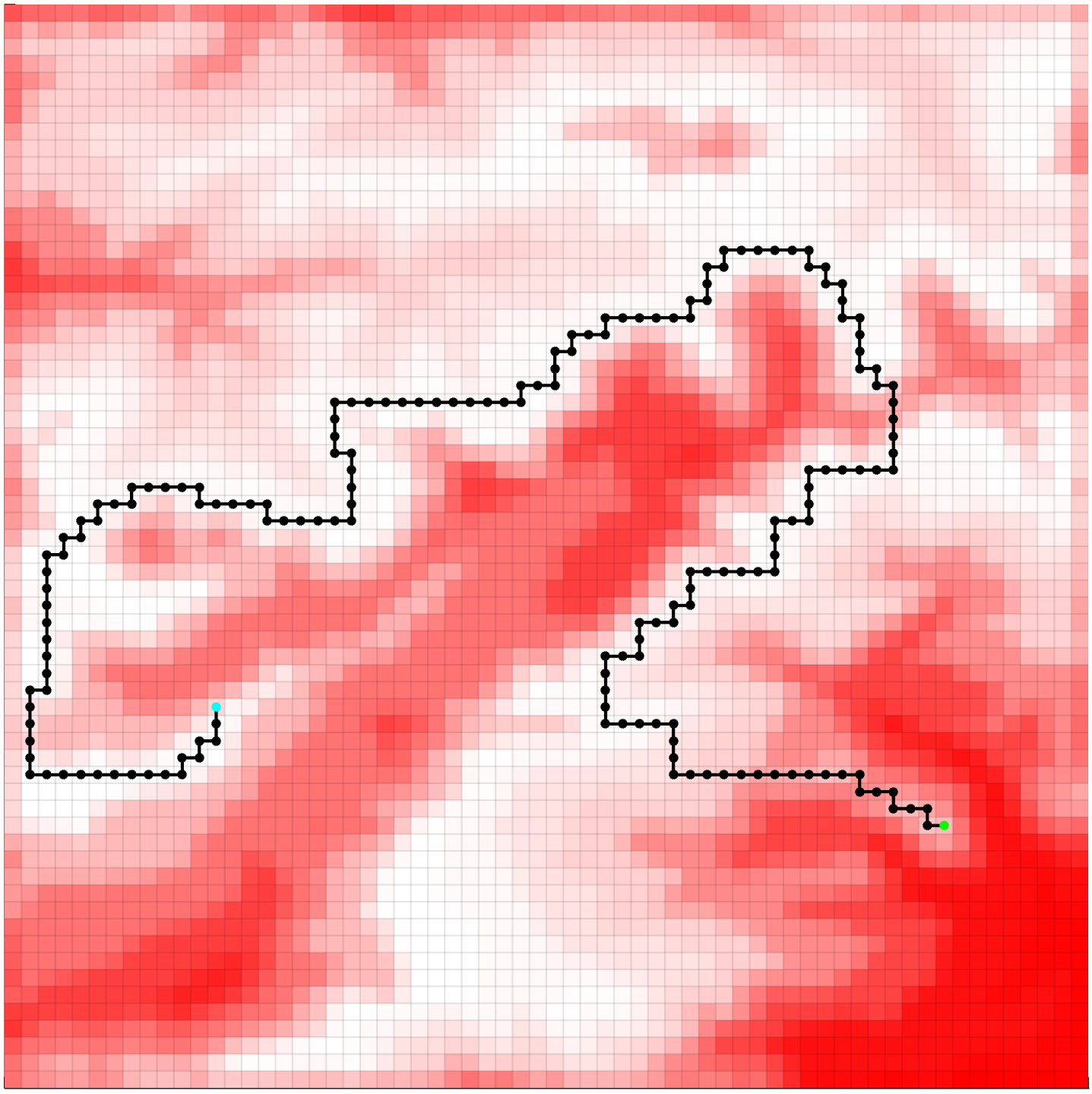
Figure 15: 64$\times$64 original map of environment with an optimal finest resolution path leading from the start location (cyan) to goal location (green) for $\varepsilon = 0.5$. Shading of red indicates the probability that a cell is occupied.
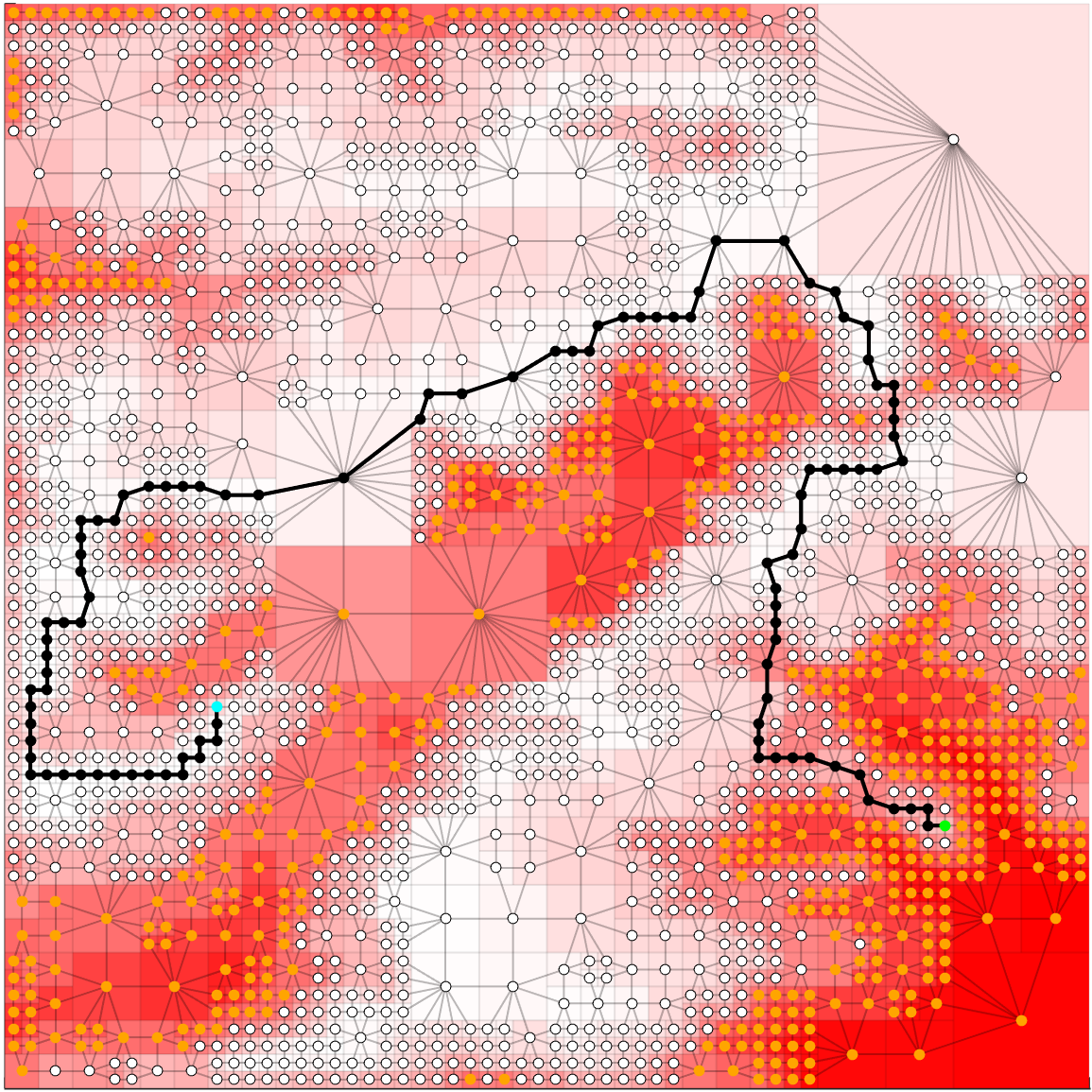
Samples of various abstract paths are shown in Figures 16-19, where each path depicted corresponds to a trade-off parameter value. In addition to displaying the resulting path, these figures also show each vertex of the associated graph, the connectivity of the graph, as well as the vertices that are considered to be $\varepsilon$-obstacles (orange). It should be noted that, in the example shown, Figure 16 depicts a path which is not considered to be $\varepsilon$-feasible, as the path traverses at least one node regarded to be an $\varepsilon$-obstacle. In addition to the results shown here, we also show, both theoretically and numerically, that the cost of the path monotonically decreases as a function of increased resolution of the environment. We also provide a discussion on the amount of compression versus the resulting optimality of the path. For these details, and for more information on this topic, see our publication here (link: link forthcoming)
Sponsors
This work has been sponsored by the Office of Naval Reserach (ONR) and the Army Research Lab (ARL) DCIST project.
Selected Publications
- Larsson, Daniel T., Daniel Braun, and Panagiotis Tsiotras. "Hierarchical state abstractions for decision-making problems with computational constraints." 2017 IEEE 56th Annual Conference on Decision and Control (CDC). IEEE, 2017.
- Tsiotras, P., "Bounded Rationality in Learning, Perception,
Decision-Making, and Stochastic Games,'' in
Handbook of Reinforcement Learning and Control, Eds: K. Vamvoudakis, Y. Wan, F. Lewis, D. Cansever, Studies in Systems, Decision and Control Series, Vol. 325, pp. 491-523, Springer, 2021.
doi:10.1007/978-3-030-60990-0 - Larsson, D., and Maity, D., and Tsiotras, P., "Information-Theoretic Abstractions for Planning for Agents with Computational Constraints," IEEE Robotics and Automation Letters, Vol. 6, No. 4, pp. 7651-7658, 2021, doi: 10.1109/LRA.2021.3099995
- Larsson, D., and Tsiotras, P., "Hierarchical
State Abstractions for Decision-Making Problems with Computational
Constraints,'' 56th IEEE Conference on Decision and Control,
Melbourne, Australia, Dec. 12--15, 2017, pp. 1138--1143, doi: 10.1109/CDC.2017.8263809

- Larsson, D., Kotsalis, G., and Tsiotras, P., "Nash and Correlated Equilibria for Pursuit- Evasion Games Under Lack of Common Knowledge,"
57th IEEE Conference on Decision and Control, Miami, FL, Dec. 17–19, 2018, pp. 3579–3584. doi:
10.1109/CDC.2018.8619168

- Guan, Y., Maity, D., Kroninger, C., and Tsiotras, P., "Bounded-Rational Pursuit-Evasion Games,'' American Control Conference, New Orleans, LA, May 26-28, 2021, pp. 3216-3221, doi: 10.23919/ACC50511.2021.9483152
- Zhang, Q., Guan, Y., and Tsiotras, P., "Learning Nash Equilibria in Zero-Sum Stochastic Games via Entropy-Regularized Policy Approximation," 30th International Joint Conference on Artificial Intelligence, Montreal, Canada, Aug. 21-26, 2021, https://arXiv:2009.00162
- Larsson, D., Maity, D., and Tsiotras, P., "A Linear
Programming Approach for Resource-Aware Information-Theoretic
Tree Abstractions,'' in Computation-aware Algorithmic Design
for Cyber-Physical Systems,
Eds: M. Prandini and R. Sanfelice, Birkhauser, 2021