Stochastic Optimal Control for Powered Descent Guidance
Entry, Descent, and Landing (EDL) is the process of guiding a spacecraft entering a planet's atmosphere, decelerating from orbit, and descending to a safe landing site on the planet's surface. Atmospheric disturbances, localization error, and other factors contribute to substantial deviations from the nominal descent trajectory that must be accounted for when selecting a landing target. This work focuses on the Powered Descent (PD) phase, during which the spacecraft uses chemical rocket engines to simultaneously steer and decelerate to a target touchdown point. NASA Technology Area (TA) 9.2.6 (Large Divert Guidance) identifies a guarantee on satisfaction of constraints, optimal or near-optimal fuel consumption, and on-board computational feasibility as necessary components of a next generation solution. In this research we are concerned with applying techniques from stochastic optimal control theory to the problem of powered descent guidance with the objective of improving fuel performance.
To motivate our approach to this problem, consider a car driving to a stop sign and suppose that the driver wishes to reach the stop sign as quickly as possible. It is not difficult to convince oneself that the best strategy to race to the stop sign is to max out the acceleration before slamming on the brakes at some precise time (i.e. bang-bang control). Now suppose that the motion of the car is disturbed along the path to the stop sign, particularly after the driver switches to using the brakes. If the disturbance speeds up the car, then the driver will be unable to bring the car to a stop before the stop sign since the time-optimal strategy leaves no room for extra corrective breaking. An animation of the car with disturbances is shown below with the undisturbed car slightly transparent for comparison.

Since the car’s motion is randomly disturbed, the position and velocity of the car become random variables. As a consequence, it is no longer possible to bring the car to a stop exactly at the stop sign since the car’s position when it stops is a random variable distributed in position. Instead, we specify a final distribution of the stopping position. In this research, this problem is solved by computing margins in planned acceleration and breaking that leave room for corrections to be made in response to disturbances. An example of the proposed method is shown below. The reference path is shown slightly transparent behind a sample path.

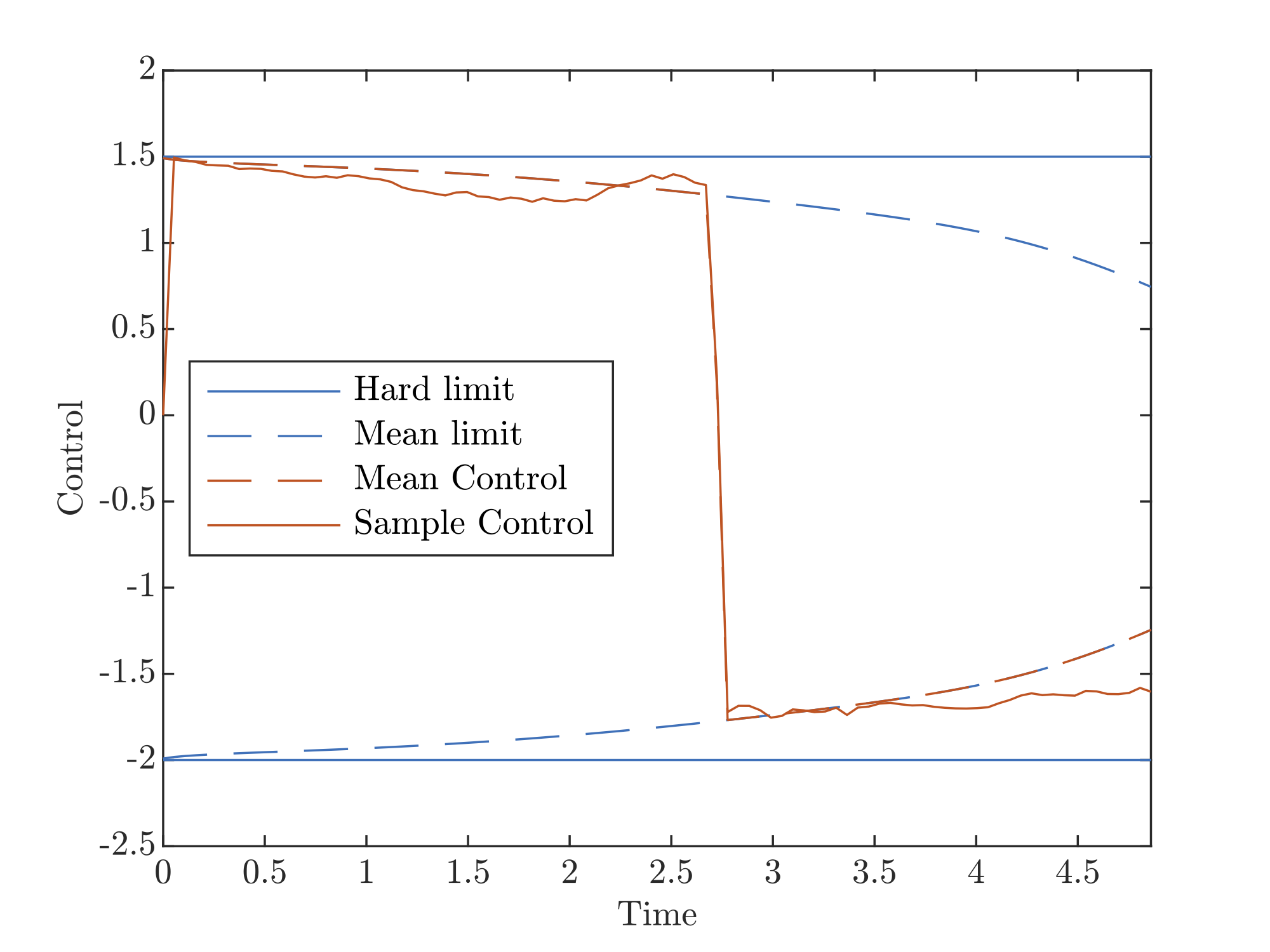
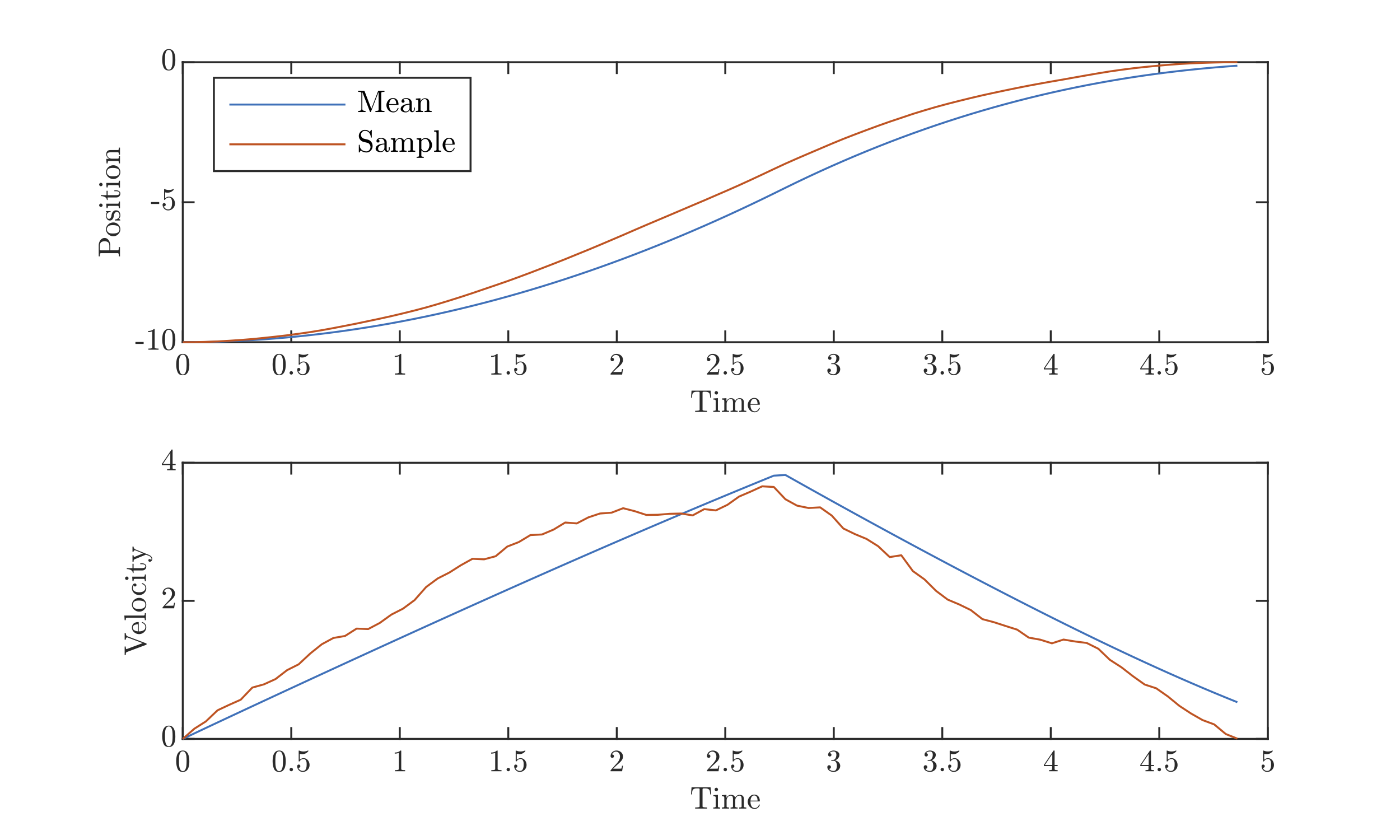
Note that the sample path, compared to the previous example, comes to a stop very near the stop sign. Plots of the motion and control for the above animation are shown below. As one might expect, the planned breaking is much less than the maximum breaking right before the stop sign to give room for final corrections.
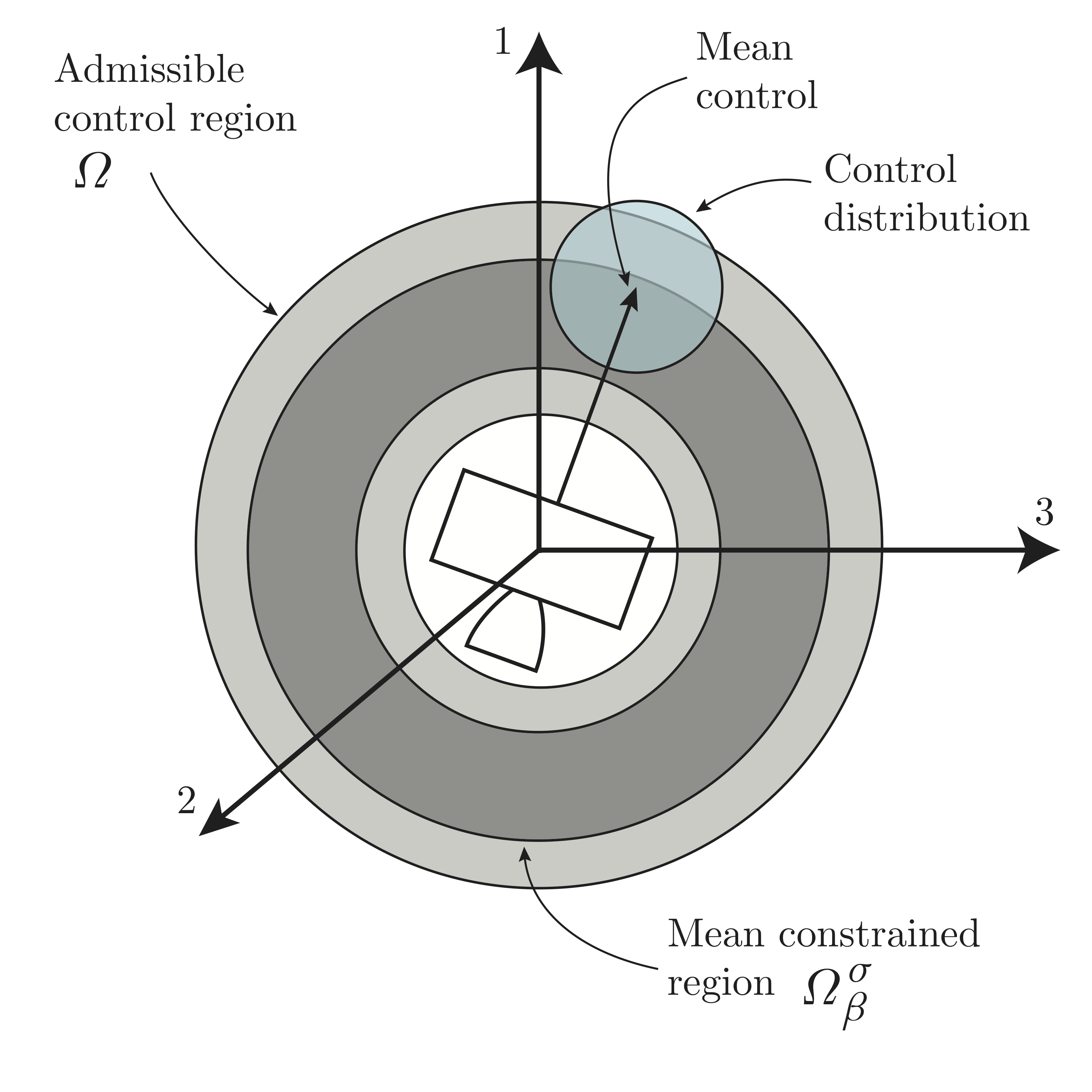
Returning now to powered descent guidance (PDG), we suppose that the spacecraft position and velocity is a random variable subject to random external forces, graphically shown below.
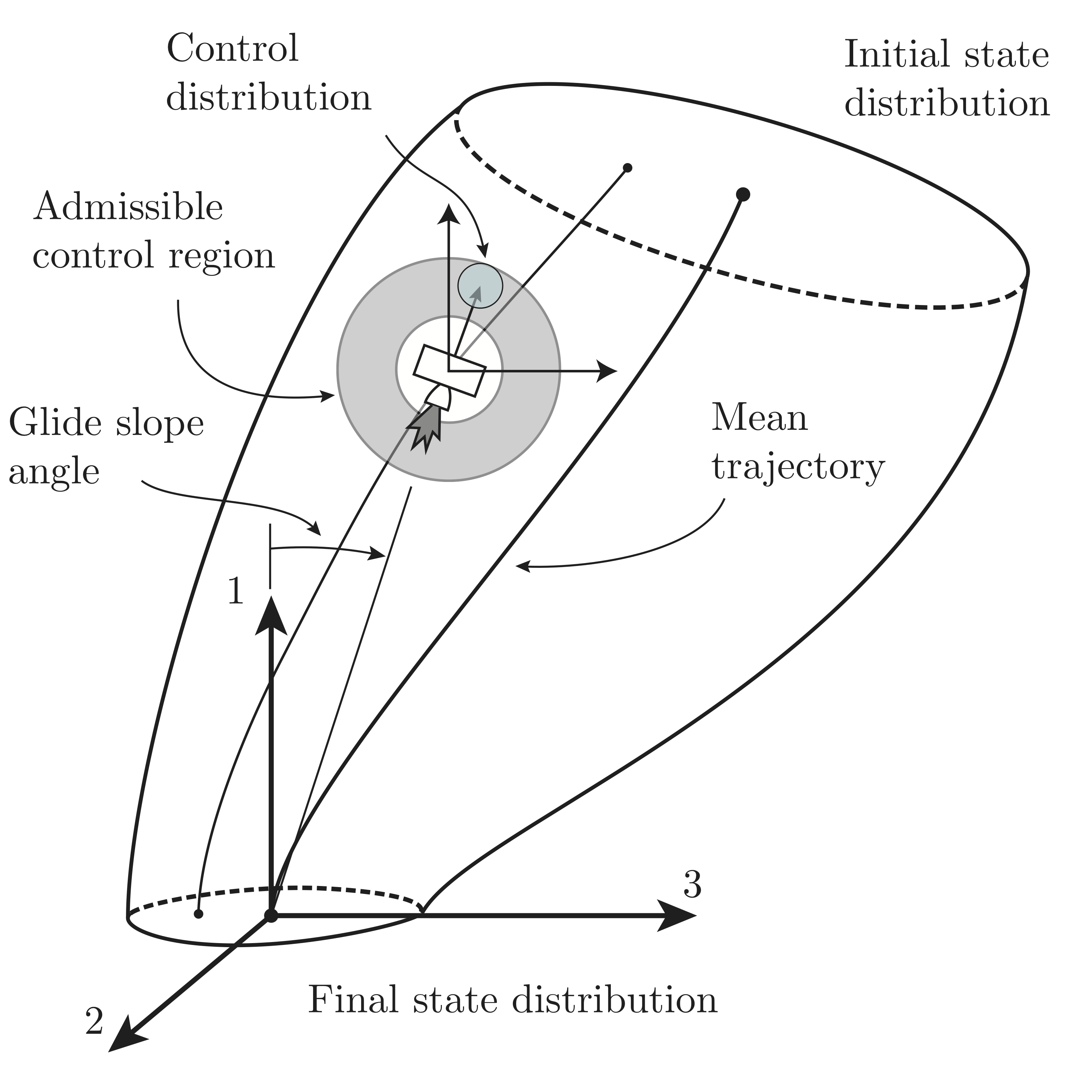
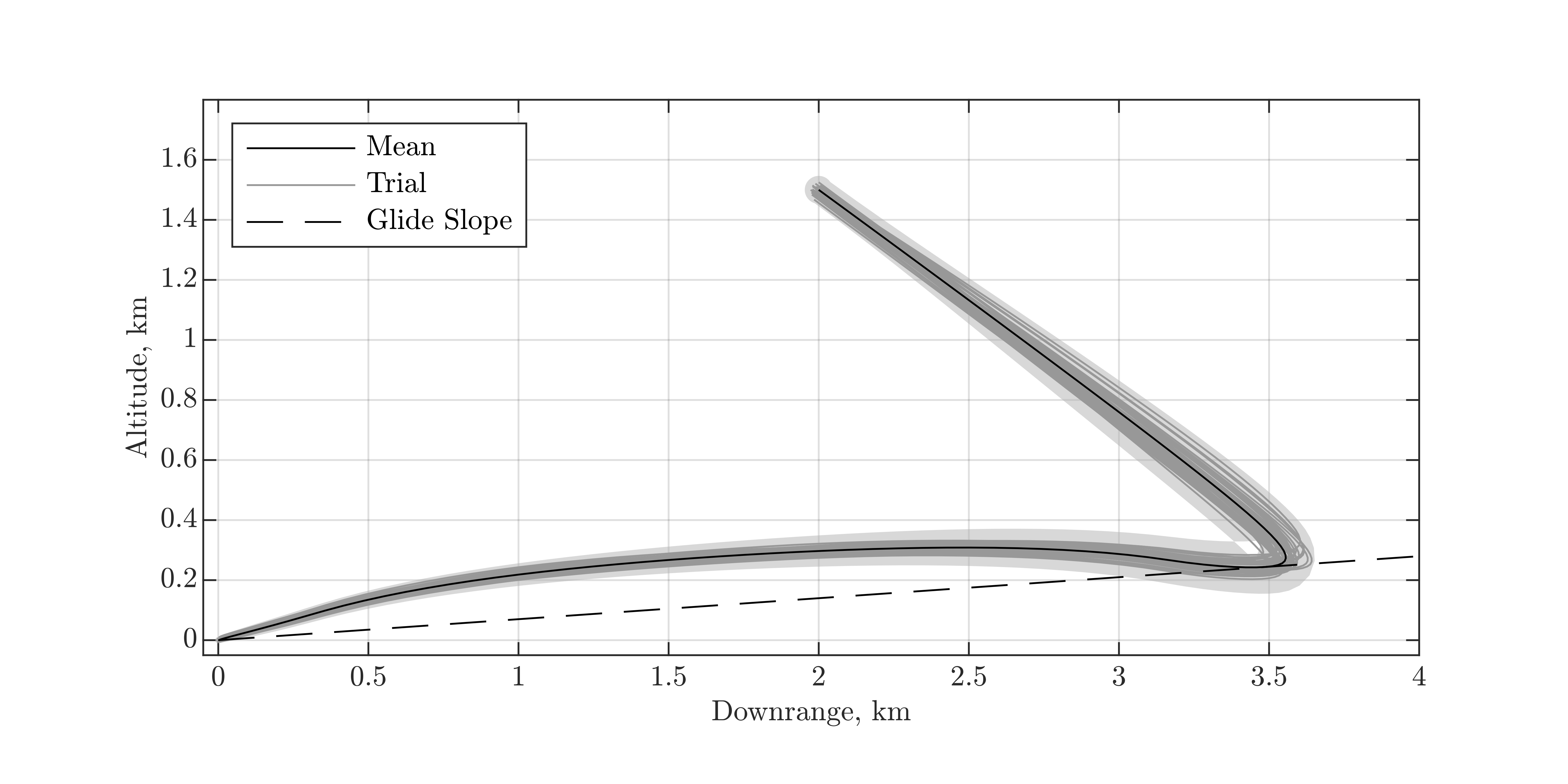
As with the car example, we want to guide the rocket to a final distribution around a landing sight. Similar to the car example, the minimum-fuel throttle solution for PDG is bang-bang, and thus it encounters the same problem with robustness to disturbances. We develop the ideas explored in the car example to find a guidance and control solution that is robust to initial state uncertainty and random external forces in our paper. Figures from a numerical example are shown below. Poster

Sponsors
This project is supported by NASA Space Technology Research Fellowship.
Selected Publications
- Ridderhof, J., and Tsiotras, P., "Uncertainty Quantification and Control During Mars Powered Descent and Landing using Covariance Steering,'' AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, Jan. 8--12, 2018.
- Ridderhof, J., and Tsiotras, P., "Minimum-fuel Powered Descent in the Presence of Random Disturbances,'' AIAA Guidance, Navigation, and Control , San Diego, CA, Jan. 7--11, 2019 (best student paper award).
- Riderhof, J., and Tsiotras, P., "Minimum-fuel Powered Descent in the Presence of Random Disturbances," AIAA Guidance, Navigation, and Control Conference, San Diego, CA, Jan. 7–11, 2019 (best student paper award). doi: 10.2514/6.2019-0646
- Ridderhof, J., and Tsiotras, P., "Stochastic Atmosphere Modeling for Risk-Adverse Aerocapture Guidance," IEEE Aerospace Conference, Big Sky, Montana, March 7-14, 2020.

