Learning Optimal Control using Forward-Backward SDEs
Stochastic optimal control has seen significant recent development, motivated by its success in a plethora of engineering applications, such as autonomous systems, robotics, neuroscience, and financial engineering. Despite the many theoretical and algorithmic advancements that made such a success possible, several obstacles remain; most notable are (i) the mitigation of the curse of dimensionality inherent in optimal control problems, (ii) the design of efficient algorithms that allow for fast, online computation, and (iii) the expansion of the class of optimal control problems that can be addressed by algorithms in engineering practice.
Prior work on stochastic control theory and algorithms mitigates the complexity of the optimal control problem by sacrificing global optimality. Furthermore, several restrictive conditions are imposed, such as differentiability of the dynamics and cost functions, as well as certain assumptions involving control authority and stochasticity. Thus, state-of-the-art algorithms may only address special classes of systems. The goal of this research is to establish a framework that goes beyond these limitations. The proposed stochastic control framework capitalizes on the innate relationship between certain nonlinear partial differential equations (PDEs) and forward and backward stochastic differential equations (FBSDEs), as demonstrated by a nonlinear version of the Feynman-Kac lemma. By means of this lemma, we are able to obtain a probabilistic representation of the solution to the nonlinear Hamilton-Jacobi-Bellman equation, expressed in form of a system of decoupled FBSDEs. This system of FBSDEs can then be solved numerically in lieu of the original PDE problem. We develop a novel discretization scheme for FBSDEs, and enhance the resulting algorithm with importance sampling, thereby constructing an iterative scheme that is capable of learning the optimal control without an initial guess, even in systems with highly nonlinear, underactuated dynamics.
The framework addresses several classes of stochastic optimal control, including $L^2$, $L^1$, game theoretic, and risk sensitive control, in both fixed-final-time as well as first-exit settings.
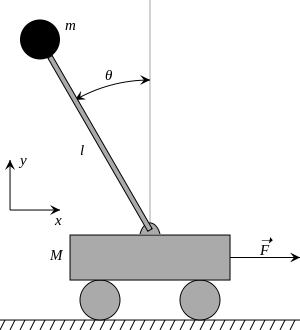
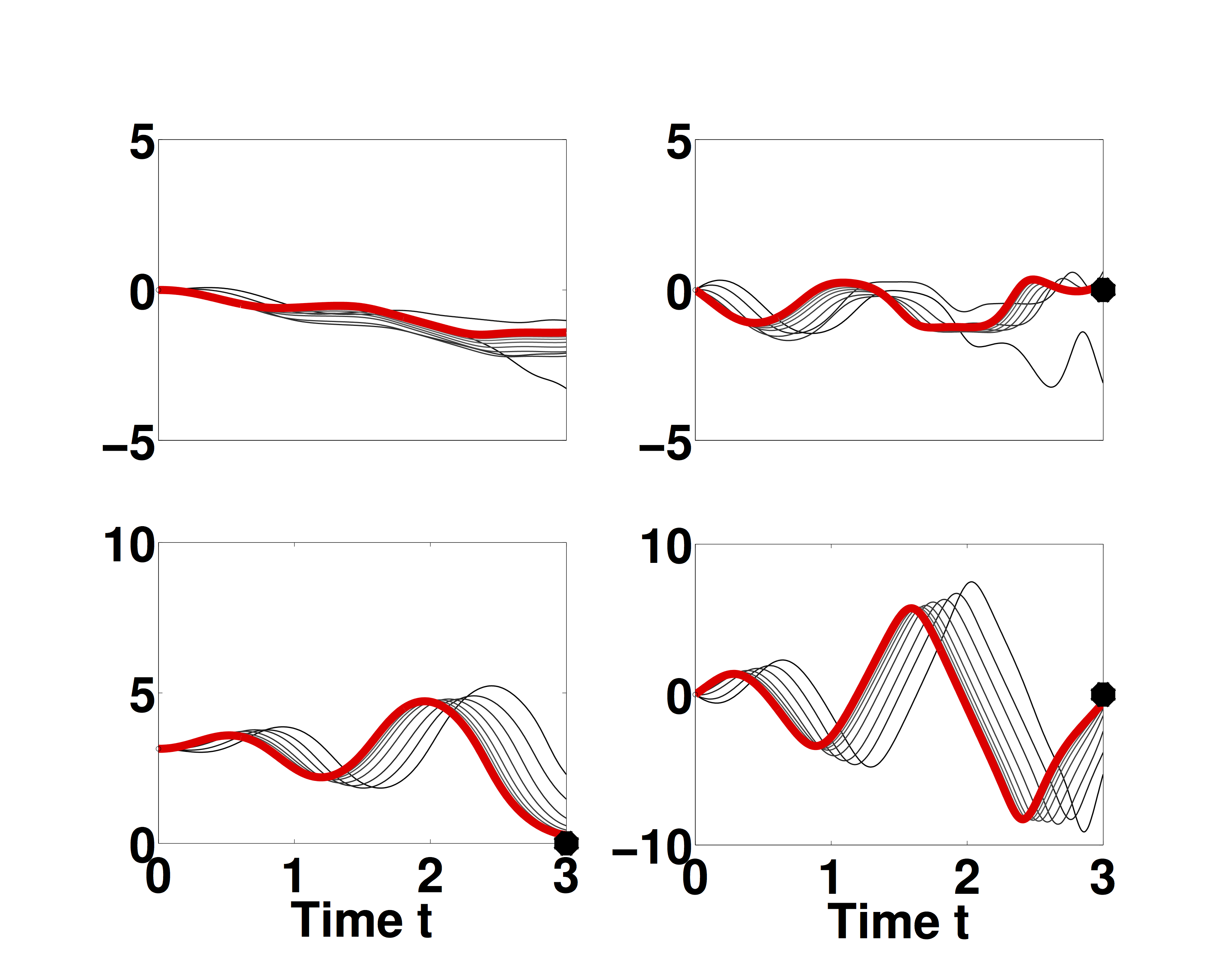
(a) Cart-pole system, where in the task is to invert the pendulum attached to the cart by moving the cart. (b) Top left- cart position, top right- cart velocity, bottom left- pole position, bottom right - pole velocity. Trajectory mean of the controlled system for each iteration (gray scale) and after the final iteration (red). The black dots represent the target states.
Sponsors
This project is supported by NSF.

