ARCHES: Autonomous Resilient Cognitive Heterogeneous Swarms
Humans appear to rely heavily on hierarchical structures for decision-making, especially for complex tasks (e.g., planning a route from work to home, navigating traffic, etc). Despite the fact that any plan is physically realizable as a sequence of refined actions (e.g., walking to the office door, opening the door, walking down the hallway, etc), most humans do not plan at this low level set of actions. Instead, planning is achieved using a variety of abstraction levels, by aggregating the sequence of actions into high level macro-actions (i.e., exiting the office building, changing lanes in traffic, etc), and by executing this sequence of high level actions by refining them down. This is done because acquiring perfect knowledge about the environment is often prohibitive, and hence acting on the right level of granularity of pertinent information is imperative in order to operate in dynamic and uncertain environments.
Although complete knowledge of the environment is necessary to plan an optimal solution for given task, the information about the world in which a planning agent is to plan is rarely entirely known. More likely, the agent has only a glimpse of the world abstracted away from the current state and time. This idea has led many researchers to wonder how to abstract the search space in an efficient and meaningful way. Since the early days of AI, a hierarchical abstraction of a transition system has been recognized as a crucial tool for planning in complex environments and long decision horizons.
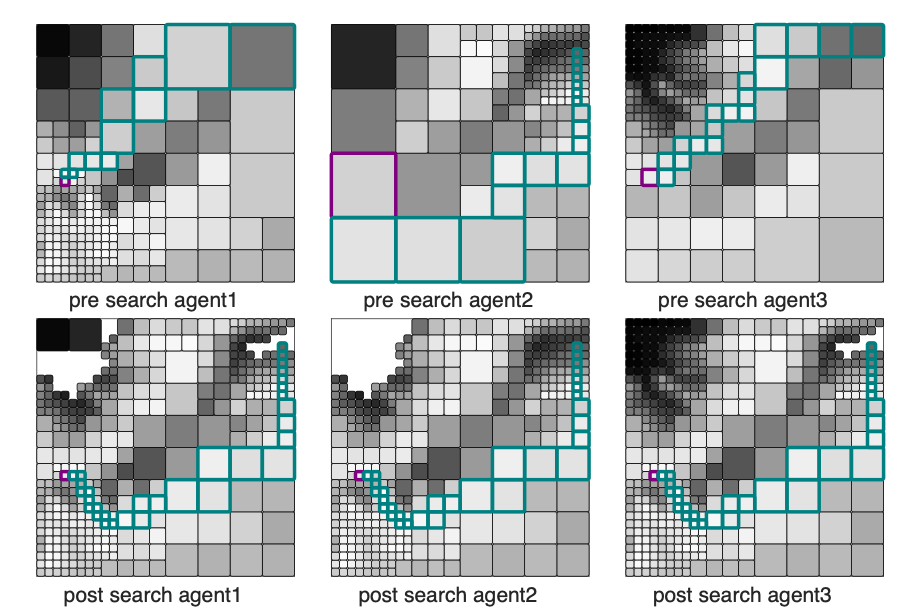
To reduce the search space and to formulate an innate perception-action loop, we use multi-resolution graph to plan. We construct fine resolution graph near the agent to accurately represent the environment in the vicinity of the agent, and coarser resolution far-away of the agent to reduce the search space. Inevitably, this multi-resolution framework may abstract some crucial information far-away from the agent, and consequently the solution quality can degrade.
But what if our agent is allowed to use other agents' finer information and vice versa to cooperatively find a better solution? If so, what would be an efficient way to communicate the information among the agents? We try to answer these questions with a distributed search algorithm. We approach this problem by refining each agent’s abstract path using the information provided by the other agents, as distributed local information provides a better heuristic to refine multi-resolution paths of agents.
The main idea is to restrict communication among the agents to just the problem-specific information needed to refine each agent’s abstract graph along the search. In this approach, the agents communicate only the expansion result of A∗ to locally rewire, and hence all agents attain a common subgraph that includes a provably optimal path in the most informative graph available among all agents if one exists, without necessarily communicating the entire graph. The solution quality and the speeds up from abstraction is balanced efficiently by using multiple agents distributed in the search space, as they communicate only the expansion result of A* to avoid unnecessary communication.
We use the idea of “bounded rationality” to capture another aspect of the cognitive heterogeneity in a group. Humans, most of time, are not fully rational. With the limited amount of time given and the limited computational power of a human brain, we tend to make decisions that are “good enough”, instead of finding the decisions that are globally optimal.
We use the classical example of the “Guess 2/3 of the average” game to motivate the bounded rationality idea. In this game, a group of human subjects are asked to pick an integer between zero and a hundred within 60 seconds. The winner is the one whose number that is the closest to the 2/3 of the average choice of the group. The Nash equilibrium of this game is zero, namely each participant should pick zero as his response, if all of the participants be totally rational. However, when this game was played among college students during a lecture on game theory, the students’ responses deviated significantly from the Nash equilibrium.
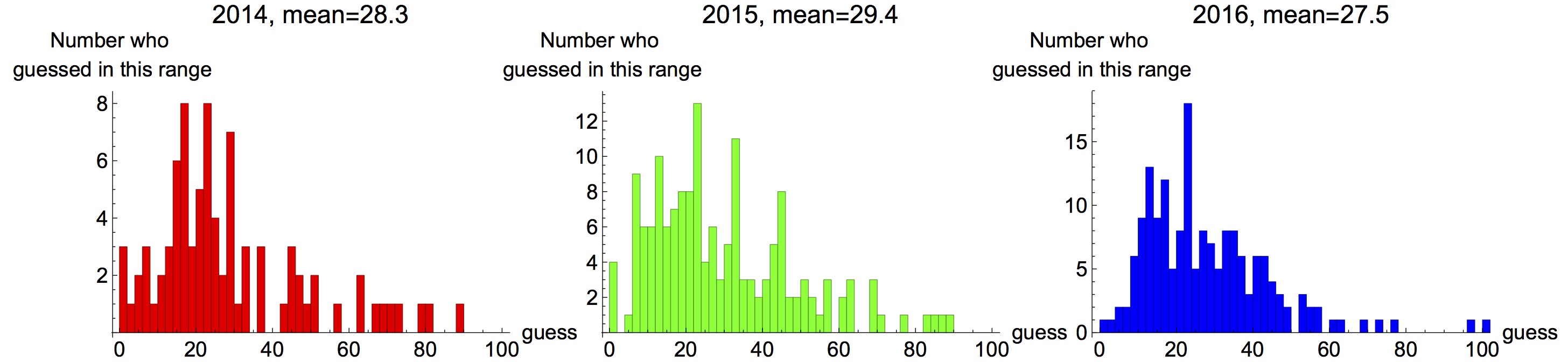
Outcome of the "Guess 2/3 of the average" game played among college students. [source: http://www.mathemafrica.org/?tag=game-theory]
The results from the “Guess 2/3 of the average game” naturally lead to another question: If an autonomous agent(s) participates in a game with agents that are not fully rational, what strategy should it pick to maximize its likelihood of winning? In this “guess 2/3” example, if the autonomous agent assumes the other agents (humans) are fully rational, it should pick the Nash equilibrium, i.e. zero, as its number selection. However, if some of the other agents pick non-zero integers (not fully rational), the autonomous agent has less chance to win this game by sticking to the Nash equilibrium. From the post-game statistics, the optimal integer the autonomous agent should pick is instead around nine or ten.
In reality, not just humans, many of the autonomous agents also have limitations on computational capacity, available information and computational time and thus cannot be fully rational. To find the optimal strategy in a game that involves agents that are not fully rational, we need to first model such agents. Many literatures use the concept of bounded rationality to describe such computational limitations/constraints that the agents face. So, is there a way to model such “irrational” decision makers?
We adopt the level-k thinking framework from the behavioral game theory literature to model the agents of bounded rationality. In the level-k framework, the level-0 agents are first defined with some naïve strategies. Then the level-1 agents best respond to their level-0 opponents, and the level-2 agents best respond to their level-1 opponents, and so on. By adopting this framework, we can put a bound on the maximum level that an agent can go for, and these agents are thus of bounded rationality.
The level-k thinking framework imitates the thinking processes of many people in the “guess 2/3” game. The level-0 players are naïve and may pick an integer as large as 100. The level-1 will then pick at most 67, since the average among all the level-0 agents can be at most 100. The level-2 players should then pick no more than 45, if it assumes its opponents are at least level-1, and so on. This iterative thinking process continues on till the human subject thinks he has “out-smarted” most of its opponents or has run out of time.
We tested this framework on a discretized pursuit-evasion game (PEG) over a 16 × 16 grid world with stochastic wind fields, as shown in the following figure.
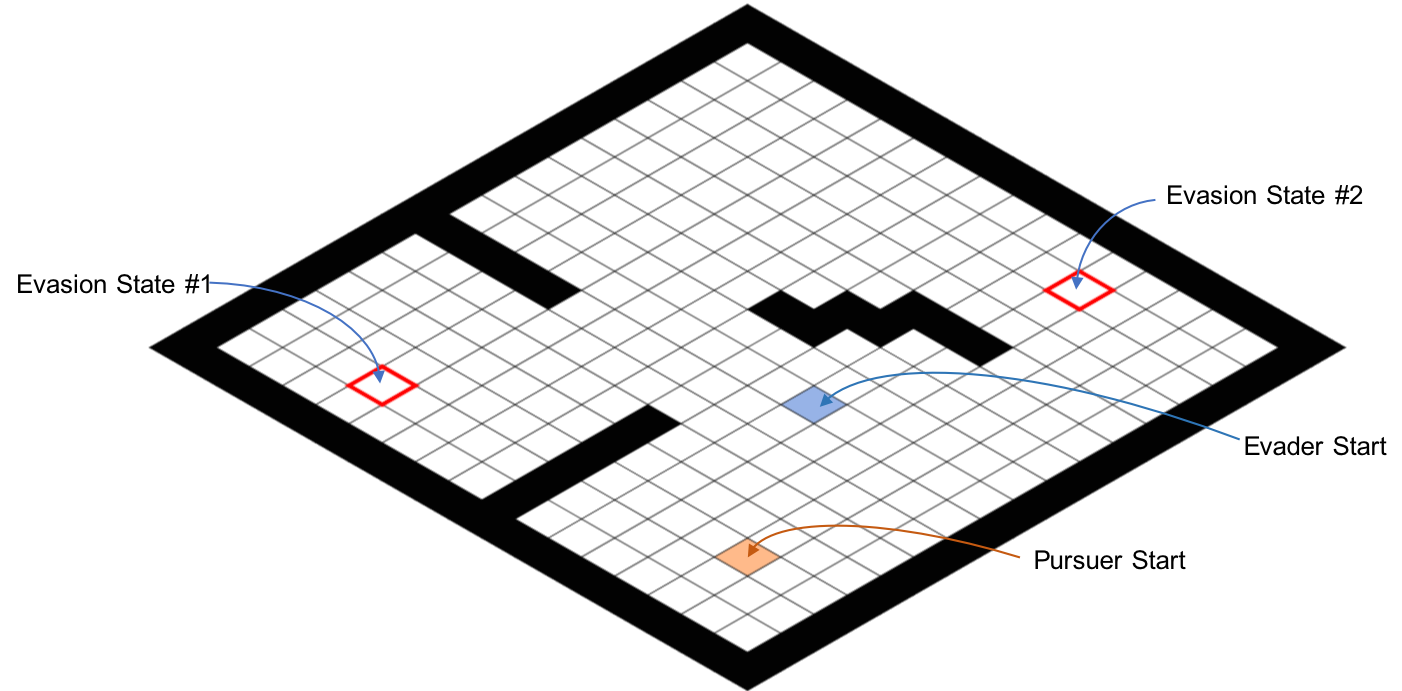
The setup of the pursuit-evasion game.
The pursuer and the evader start at the cells marked with orange and blue respectively. An evasion is successful when the evader enters one of the two evasion-states. The black cells are the obstacles, and the agent that enters these cells is considered crashed and loses the game immediately. The following sample trajectory illustrates how the level-k thinking framework functions in our PEG.
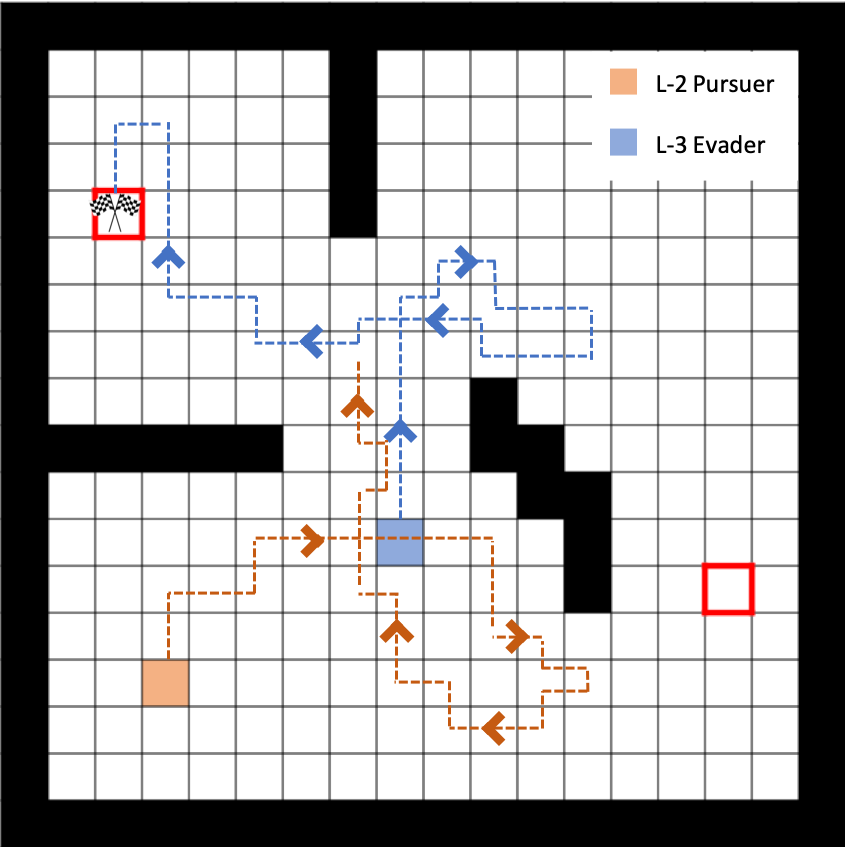
A sample trajectory, a level-2 pursuer vs. a level-3 evader. The evader successfully evades in the trajectory presented.
In the sample trajectory presented is a PEG between a level-2 pursuer and a level-3 evader, and the evader evades in evasion-state #1. One can observe the "deceiving" behavior of the evader: the level-3 evader out-smarts its level-2 opponent by first heading right and then suddenly turning left. This move tricks the level-2 pursuer to believe that the intension of the evader is to go to the evasion-state #2 on the right. As a result, the level-2 pursuer goes right and takes the “short cut” beneath the obstacles to defend the evasion-state #2. Then, the evader suddenly turns left and go to the evasion-state #1 on the left. At the time when the evader reveals its true intension to go to evasion-state #1, the distance between the evader and the pursuer is already large and the chance of the pursuer capturing the evader is significantly decreased. This sample trajectory demonstrates how an autonomous agent would respond, if it takes the bounded rationality of its opponent into account while computing its strategy.
Sponsors
This project is funded by ARL.
Selected Publications
- Larsson, Daniel T., Daniel Braun, and Panagiotis Tsiotras. "Hierarchical state abstractions for decision-making problems with computational constraints." 2017 IEEE 56th Annual Conference on Decision and Control (CDC). IEEE, 2017.
- Tsiotras, P., "Bounded Rationality in Learning, Perception,
Decision-Making, and Stochastic Games,'' in
Handbook of Reinforcement Learning and Control, Eds: K. Vamvoudakis, Y. Wan, F. Lewis, D. Cansever, Studies in Systems, Decision and Control Series, Vol. 325, pp. 491-523, Springer, 2021.
doi:10.1007/978-3-030-60990-0 - Larsson, D., and Maity, D., and Tsiotras, P., "Information-Theoretic Abstractions for Planning for Agents with Computational Constraints," IEEE Robotics and Automation Letters, Vol. 6, No. 4, pp. 7651-7658, 2021, doi: 10.1109/LRA.2021.3099995
- Larsson, D., and Tsiotras, P., "Hierarchical
State Abstractions for Decision-Making Problems with Computational
Constraints,'' 56th IEEE Conference on Decision and Control,
Melbourne, Australia, Dec. 12--15, 2017, pp. 1138--1143, doi: 10.1109/CDC.2017.8263809

- Larsson, D., Kotsalis, G., and Tsiotras, P., "Nash and Correlated Equilibria for Pursuit- Evasion Games Under Lack of Common Knowledge,"
57th IEEE Conference on Decision and Control, Miami, FL, Dec. 17–19, 2018, pp. 3579–3584. doi:
10.1109/CDC.2018.8619168

- Guan, Y., Maity, D., Kroninger, C., and Tsiotras, P., "Bounded-Rational Pursuit-Evasion Games,'' American Control Conference, New Orleans, LA, May 26-28, 2021, pp. 3216-3221, doi: 10.23919/ACC50511.2021.9483152
- Zhang, Q., Guan, Y., and Tsiotras, P., "Learning Nash Equilibria in Zero-Sum Stochastic Games via Entropy-Regularized Policy Approximation," 30th International Joint Conference on Artificial Intelligence, Montreal, Canada, Aug. 21-26, 2021, https://arXiv:2009.00162
- Larsson, D., Maity, D., and Tsiotras, P., "A Linear
Programming Approach for Resource-Aware Information-Theoretic
Tree Abstractions,'' in Computation-aware Algorithmic Design
for Cyber-Physical Systems,
Eds: M. Prandini and R. Sanfelice, Birkhauser, 2021 - Lim, J., and Tsiotras, P., "MAMS-A*: Multi-Agent Multi-Scale A*,'' International Conference on Robotics and Automation, Paris, France, May 31-June 4, 2020, doi: 10.1109/ICRA40945.2020.9197045
- Guan, Y., Zhou, M., Pakniyat, A., and Tsiotras, P. "Shaping Large Population Agent Behaviors Through Entropy-Regularized Mean-Field Games,'' American Control Conference, Atlanta, GA, June 8-10 , 2022
- Lim, J., and Tsiotras, P., "A Generalized A* Algorithm for Finding Globally Optimal Paths in Weighted Colored Graphs," International Conference on Robotics and Automation, Xi'an, China, May 30-June 5, 2021, doi:10.1109/ICRA48506.2021.9561135
- Lim, J., Salzman, O., and Tsiotras, P., "Class-Ordered LPA*: An Incremental-Search Algorithm for Weighted Colored Graphs,'' IEEE/RSJ International Conference on Intelligent Robots and Systems, Prague, Czech Republic, Sept. 27-Oct. 1, 2021, doi: 10.1109/IROS51168.2021.9636736
External Links

